Ricerca IDA*

La ricerca IDA* è un algoritmo di ricerca informata che combina le caratteristiche dell'algoritmo A* con quelle di un algoritmo iterativo di ricerca in profondità ID ( Iterative Deepening ). La sigla IDA* significa letteralmente Iterative Deepening A*. A differenza degli algoritmi di ricerca in profondità ( ID ) nel caso dell'algoritmo IDA* il valore di taglio non è determinato dal limite di profondità ma dal limite di costo. L'algoritmo IDA* appartiene alla categoria degli algoritmi di ricerca euristica con memoria limitata poiché consente di ridurre l'utilizzo dello spazio di memoria, rispetto a un algoritmo di ricerca A*, in quanto non deve ricordare tutti i nodi visitati ma soltanto un percorso alla volta. Lo spazio di complessità è lineare. L'algoritmo IDA* viene proposto da Korf nel 1985

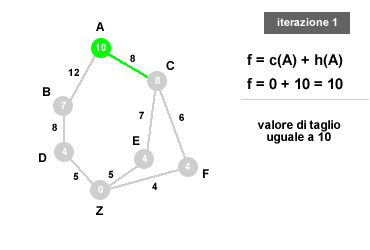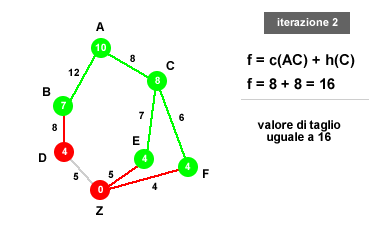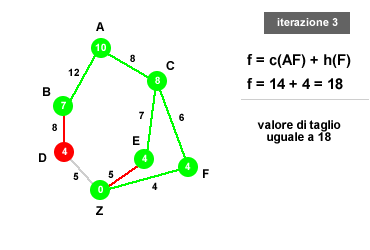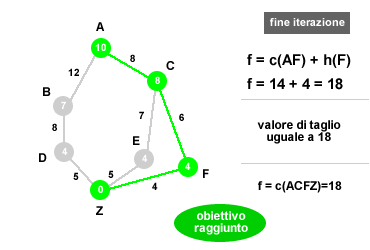
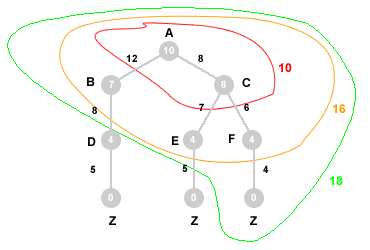
Esempio ricerca IDA*. Nel precedente grafo l'algoritmo deve esplorare il percorso meno costoso per giungere da A (partenza) a Z (obiettivo). In ogni nodo è indicata la distanza aerea tra il relativo nodo e la destinazione finale (Z) mentre il numero tra gli archi indica la distanza stradale reale tra i due nodi dell'arco. Ad esempio, la distanza stradale (valore reale) tra A e B è pari a 12 mente la distanza aerea (valore euristico) da B a Z è pari a 7. L'algoritmo deve minimizzare il costo del percorso.

• Prima iterazione. Nel primo ciclo il valore di taglio è determinato dalla somma minima tra il valore reale C e il valore stimato H (euristico) a partire dal nodo di partenza A. Essendo C(A) uguale a zero, il primo valore di taglio ( costo limite ) è individuato dalla funzione euristica H(A)=10. Tutte le ricerche in profondità con costo superiore a 10 sono interrotte ( backtracking ). L'obiettivo non è stato raggiunto. Il migliore percorso è al momento AC.
• Seconda iterazione. Nel secondo ciclo il valore di taglio è determinato dalla migliore continuazione del percorso AC. Il nuovo valore di taglio è individuato dalla somma del costo reale per raggiungere C (il nodo migliore dell'iterazione precedente) a partire da A (nodo iniziale) con il valore euristico per raggiungere Z da C. Il nuovo valore di taglio è, quindi, determinato dalla somma C(AC)+H(C) = 8 + 8 = 16. Nella seconda iterazione tutte le ricerche in profondità con costo superiore a 16 sono interrotte. L'obiettivo non è stato raggiunto. Il migliore percorso è al momento ACF.
• Terza iterazione. Nella terza iterazione il valore di taglio è determinato dalla somma dei costi reali per raggiungere F (il nodo migliore dell'iterazione precedente) a partire da A (nodo iniziale) con il valore euristico per raggiungere Z da F. Il nuovo valore di taglio è, quindi, determinato dalla somma C(AF)+H(F) = 14 + 4 = 18. Nella terza iterazione tutte le ricerche in profondità con costo superiore a 18 sono interrotte. L'obiettivo è stato raggiunto.
• Obiettivo raggiunto. Nella terza iterazione l'algoritmo trova un percorso da A a Z con costo non superiore al valore di taglio (18). Si tratta del percorso ACFZ con costo pari a 18. Non essendoci vie alternative migliori l'algoritmo termina l'esecuzione restituendo come soluzione il percorso ACFZ.

Il funzionamento dell'algoritmo IDA* può essere analizzato anche tramite i relativi stati su un albero di ricerca. I confini (contour) tracciati sull'albero di ricerca sono simili alle linee topografiche e rappresentano il valore di taglio adottato dall'algoritmo in ogni ciclo ( iterazione ).

Come si può notare il valore di taglio dell'algoritmo Iterative Deepening A* non è determinato dalla reale profondità dei nodi nell'albero di ricerca ( algoritmo ad approfondimento iterativo ) ma dal costo minimo ( costo limite ) della funzione euristica del costo (C+H). L'algoritmo agisce come un algoritmo di ricerca informata A* ( ricerca a stella ) poiché stima il valore euristico della distanza tra ciascun nodo e il nodo finale e a ogni iterazione la ricerca in profondità viene interrotta per valori di costo superiori alla funzione di costo (C+H).

Complessità spaziale. Il principale vantaggio di una ricerca IDA* è il minore spazio di memoria rispetto a una ricerca informata A*. Nel caso della ricerca IDA* l'algoritmo deve registrare soltanto l'ultimo percorso migliore e il valore di taglio. La ricerca dei percorsi alternativi avviene in profondità e si interrompe al raggiungimento del valore di taglio (costo del percorso migliore). A ogni iterazione il valore di taglio è determinato dalla funzione euristica ( distanza reale + distanza stimata ). In conclusione, l'algoritmo IDA* vanta una minore complessità spaziale a parità di completezza rispetto a un algoritmo di ricerca A*.

Complessità temporale. L'algoritmo IDA* presenta gli stessi handicap di una ricerca iterativa in profondità. In particolar modo, il tempo di esecuzione potrebbe diventare proibitivo in caso di problemi molto complessi. A ogni iterazione l'algoritmo scandaglia nuovamente gli stessi percorsi già analizzati fino al valore di taglio. La complessità temporale può aumentare in modo esponenziale a ogni ulteriore iterazione.

Limitazioni iterazione in profondità. In caso di problemi molto complessi è possibile indicare una funzione euristica in cui la ricerca nei valori reali sia limitata entro una determinata profondità, lasciando tutto il resto ai valori stimati. L'algoritmo potrebbe restituire soluzioni sub-ottimali ma in tempi di elaborazione più brevi. Questo escamotage consente di ridurre la complessità temporale dell'algoritmo sacrificando, tuttavia, la completezza della ricerca della soluzione. Inoltre, non è escluso di incappare nei vincoli ciechi se l'euristica non è ottimale.