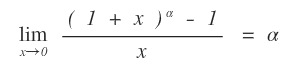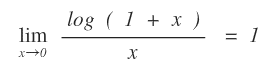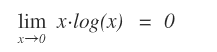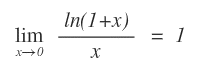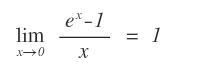Limiti notevoli

I limiti notevoli sono forme indeterminate particolarmente ricorrenti che consentono di calcolare altri limiti più complessi.

Ogni limite notevole è ottenuto svolgendo una serie di passaggi matematici. Questi passaggi sono detti dimostrazione del limite notevole.

Esempio di limite notevole

Il seguente limite per x→0 è una forma di indecisione del tipo 0/0.

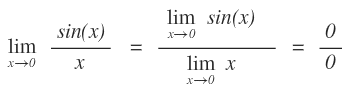
Quindi non è possibile calcolare immediatamente il limite della funzione.

Tuttavia, svolgendo opportuni calcoli algebrici è possibile dimostrare che questo limite è uguale a 1.

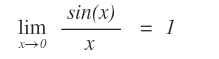
Questo è un esempio di limite notevole.

A cosa servono i limiti notevoli? Una volta imparati a memoria, i limiti notevoli possono essere usati per calcolare rapidamente i limiti di molte altre funzioni equivalenti, senza dover svolgere ogni volta la dimostrazione matematica ( esempio pratico ).

I principali limiti notevoli

I principali limiti notevoli sono i seguenti:

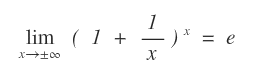
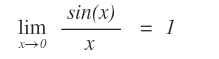
Vedi la dimostrazione.

Limiti notevoli fondamentali. Questi due limiti sono anche detti limiti notevoli fondamentali, perché permettono di dedurre molti altri limiti notevoli.

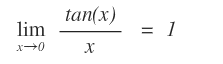
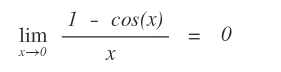
Vedi la dimostrazione

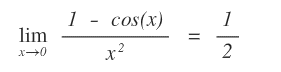
Vedi la dimostrazione