Dimostrazione del limite notevole del seno
Secondo la formula del limite notevole del seno, il limite per x che tende a zero del rapporto fra la funzione seno e la variabile incognita x è uguale a uno.
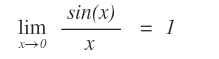
Dimostrazione
Per dimostrare il limite notevole del seno, prendiamo in considerazione il cerchio trigonometrico e un angolo positivo di ampiezza x.
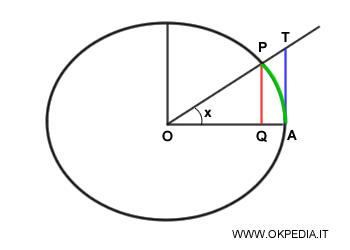
La variabile x è misurata in radianti. Quindi, la sua misura coincide con il segmento AP della circonferenza.
La misura del seno è invece coincidente alla lunghezza del segmento PQ mentre la tangente al segmento TA.
Si può facilmente vedere che i segmenti non sono uguali.
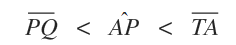
Quindi, possiamo riscrivere la diseguaglianza nel seguente modo:
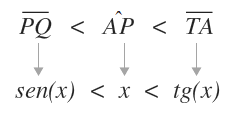
Ora dividiamo i termini della diseguaglianza per sen(x)
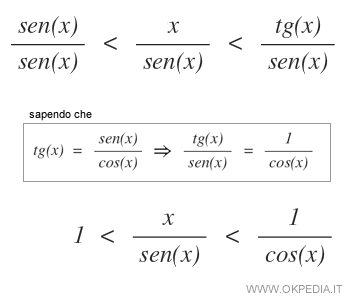
Passando ai reciproci otteniamo la seguente diseguaglianza
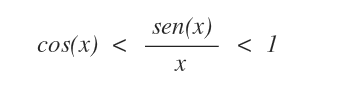
Adesso calcoliamo il limite dei termini estremi della diseguaglianza.
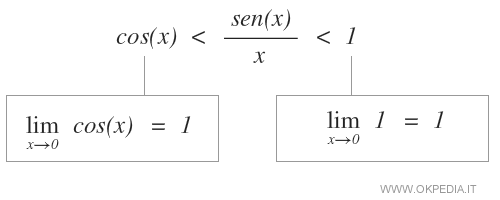
Entrambi i limiti per x→0 sono uguali a 1.
Essendo compresa tra due funzioni con limiti che tendono 1 per x→0, secondo il teorema del confronto dei limiti anche la funzione sen(x)/x ha il limite uguale a 1 per x→0.
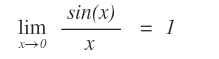
Abbiamo così dimostrato il limite notevole del seno.

