Teorema del confronto dei limiti
Se due funzioni f(x) e g(x) hanno lo stesso limite l per x che tende a un numero c ( finito o infinito ) ed esiste un'altra funzione z(x) e un intorno U(c) tale che f(x)≤z(x)≤g(x), allora anche il limite della funzione z(x) è uguale a l per x che tende a c, escluso al più x=c.

Il teorema del confronto dei limiti è anche detto il teorema dei due carabinieri perché il grafico della terza funzione z(x) è compreso tra i grafici delle funzioni f(x) e g(x) che hanno lo stesso limite l per x→c.
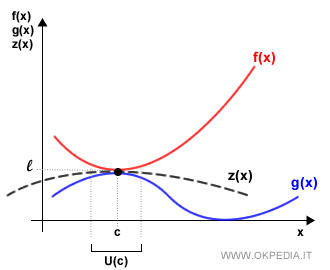
Un esempio pratico
Esempio 1
Le seguenti due funzioni f(x) e g(x) hanno lo stesso limite (l=0) per x→1
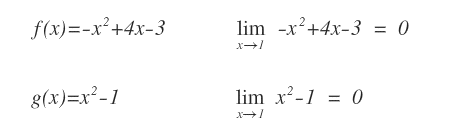
Vogliamo capire se una terza funzione z(x) soddisfa la regola del teorema del confronto nell'intorno di x=1.
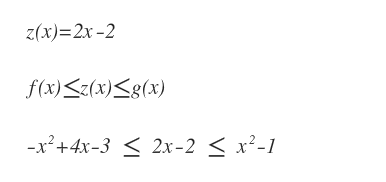
Si tratta di un sistema composto da due disequazioni.
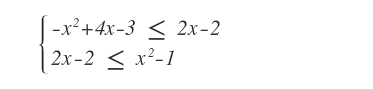
Svolgendo i calcoli algebrici vediamo che il sistema è verificato per ogni numero reale.
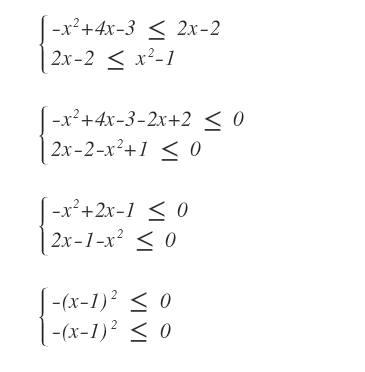
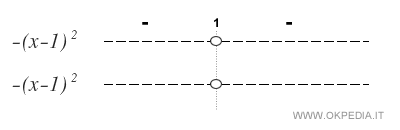
Se la diseguaglianza f(x)<z(x)<g(x) è verificata per qualsiasi numero reale xSe la diseguaglianza f(x)≤z(x)≤g(x) è verificata per qualsiasi numero reale, allora è verificata anche nell'interno di x=1.
Pertanto, essendo soddisfatte le ipotesi del teorema del confronto, possiamo affermare che il limite di z(x) è uguale a zero per x→1.
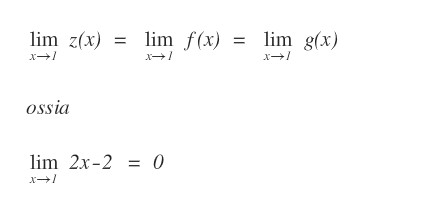
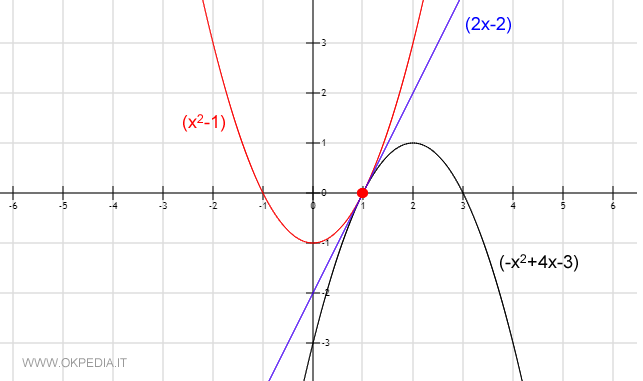
Nota. Per una verifica rapida osserviamo il grafico delle tre funzioni. Tutte le funzioni hanno un limite finito uguale a zero per x tendente a 1.
Esempio 2
Proviamo a determinare il limite per x tendente a infinito della seguente funzione z(x) usando il metodo del confronto.
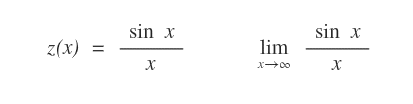
Sapendo che la funzione seno oscilla tra -1 e 1.
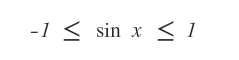
dividiamo queste diseguaglianze per l'incognita x
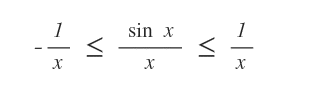
Abbiamo così ottenuto le due funzioni f(x)=-1/x e g(x)=1/x.
Ora calcoliamo il limite delle funzioni f(x) e g(x).
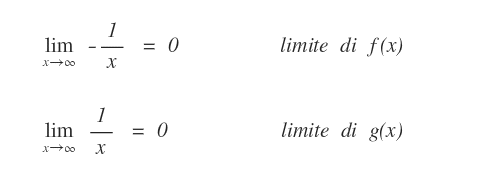
Quindi per il teorema del confronto possiamo affermare che anche il limite di z(x) è uguale a zero.
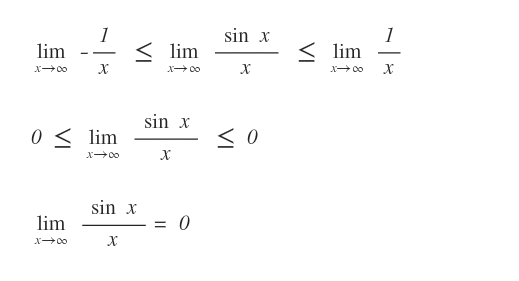
Il semplice confronto con le funzioni f(x) e g(x) ha consentito di calcolare il limite della funzione z(x).

