Il rapporto tra polinomi con limite indeterminato
Nel caso del quoziente di due funzioni polinomio P(x) e Q(x), le forme di indecisione si affrontano in modo diverso.
Esempio. Un esempio di rapporto tra due polinomi.
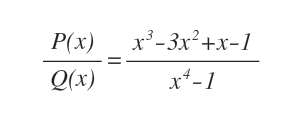
Occorre distinguere tra due casi, il limite per x tendente a infinito e quello per x tendente a un numero reale c.
Soluzione 1
Se il limite per x tendente a infinito del rapporto tra due polinomi è una forma di indecisione infinito su infinito (∞/∞)
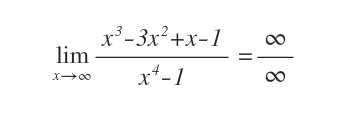
si raccolgono i termini preponderanti dei due polinomi sia al numeratore che al denominatore, rispettivamente x3 e x4.
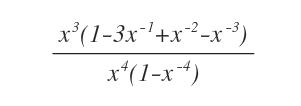
Poi si calcola il limite del rapporto tra i termini preponderanti.
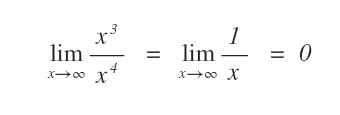
In questo modo, si può superare eventualmente la forma di indecisione (∞/∞) e calcolare il limite del rapporto tra polinomi.
Soluzione 2
Se il limite per x tendente al numero reale c del rapporto di due polinomi è una forma di indecisione zero su zero (0/0)
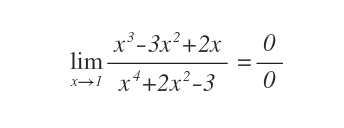
Entrambi i polinomi sono uguali a zero per x=1.
Quindi, si può usare il teorema di Ruffini su entrambi i polinomi per raccogliere il fattore (x-c) ossia (x-1).
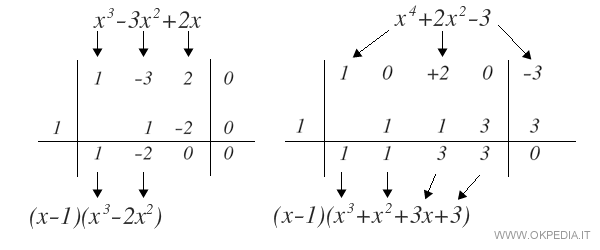
Il fattore (x-1) compare sia al numeratore che al denominatore.
Quindi si può semplificare e ridurre il grado dei polinomi.
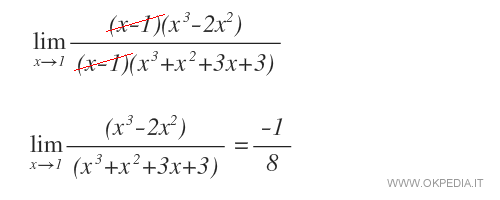
Poi si calcola il limite del rapporto tra i due polinomi ridotti.
Il limite del rapporto P(x)/Q(x) per x tendente a 1 è uguale -1/8.
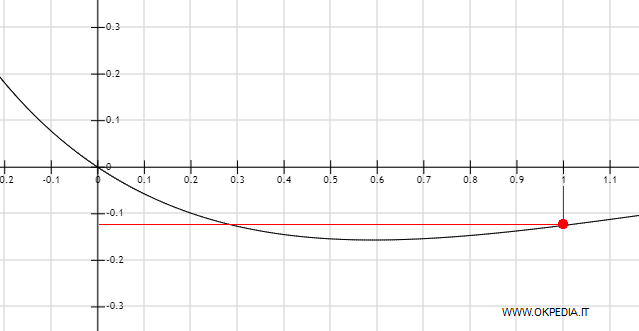
In questo modo si può eventualmente superare la forma di indecisione iniziale e calcolare il limite per x tendente a c.
Nota. In molti casi si deve ridurre i polinomi più volte fino a giungere a un limite determinato oppure a un rapporto di grado inferiore non ulteriormente semplificabile.

