Inferenza con le catene di Markov
Le tecniche di inferenza tramite le catene di Markov sono realizzate mediante algoritmi Monte Carlo, chiamato così per la loro caratteristica di effettuare delle assegnazioni di valori casuali alle variabili del sistema. Sono conosciuti anche come algoritmi MCMC ( Monte Carlo Markov Chain ).
Come funziona l'inferenza sulle catene di Markov
A partire da una rete bayesiana, composta da nodi ( variabili ) e da archi ( relazioni di indipendenza ), nella prima iterazione l'algoritmo può agire nei seguenti modi:
- Assegna a tutte le variabili un valore casuale
- Comincia da un'assegnazione determinata
Nel primo caso, l'algoritmo assegna a tutte le variabili del problema un valore casuale, tenendo conto delle relazioni di dipendenza. Nel secondo caso, invece, è l'analista a indicare all'algoritmo da quale situazione di partenza deve iniziare.
Qualunque sia la strada iniziale, l'algoritmo si trova dinnanzi a uno spazio degli stati iniziale, a cui a ciascuna variabile è assegnato un particolare valore di partenza.
Successivamente l'algoritmo comincia a effettuare le iterazioni. In ogni iterazione assegna un valore casuale a una sola variabile del problema. Tutte le altre variabili del problema sono costanti.
Per evitare i problemi di consistenza, l'algoritmo modifica soltanto le variabili non di prova. Le variabili di prova, quelle che determinano le condizioni dell'elaborazione sono lasciate costanti.
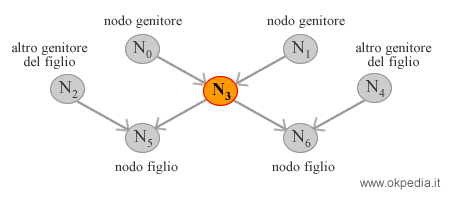
Il campionamento casuale del valore della variabile X è condizionato ai valori correnti di tutte le altre variabili della catena di Markov, ossia ai suoi nodi genitori, ai suoi nodi figli e agli altri genitori dei nodi figli.
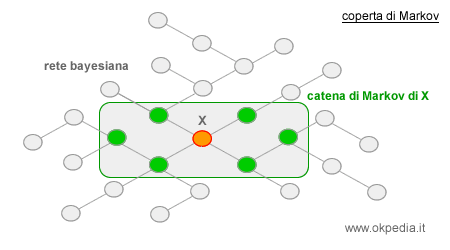
Entro la sua catena di Markov il nodo modificato ( variabile ) è condizionalmente indipendente da tutti gli altri nodi della rete che, pertanto, possono essere ignorati. Viene così a realizzarsi un equilibrio dinamico basato sulla modifica di una sola variabile alla volta.
Il nuovo valore assegnato al nodo N3 è in funzione dei valori degli altri nodi della catena di Markov. In questo modo, il nuovo valore assegnato è generalmente quello più probabile, data la probabilità condizionata all'attuale distribuzione dei valori nella catena di Markov.
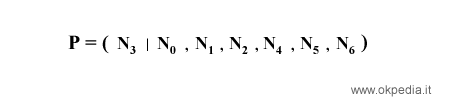
In particolar modo, la probabilità del nodo N3 nello spazio degli stati successivo è proporzionale alla sua probabilità condizionata a quella dei nodi genitori ( N0 e N1 ) moltiplicata per le probabilità dei nodi figli ( N5, N6 ) dati i loro genitori ( N2 e N4 ).
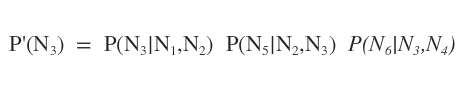
Dopo ogni iterazione lo spazio passa da uno stato all'altro. Poiché il passaggio dipende dalle probabilità condizionate, tendono a presentarsi maggiormente gli stati con la probabilità a posteriori più alta. La tecnica di campionamento basata sulla catena di Markov è, pertanto, consistente ed efficace.
Al termine di ogni iterazione l'algoritmo registra il risultato sulla variabile finale, quella di cui si vuole calcolare la probabilità di esistenza.
Dopo N iterazioni, l'algoritmo calcola la media dei valori ottenuti dalla variabile risultato, in rapporto al numero delle iterazioni.
Un esempio pratico di inferenza
A partire dalla seguente rete bayesiana e da una particolare distribuzione dei valori alle variabili, si pone al sistema la seguente domanda "Se il prezzo del petrolio aumenta, si ridurranno gli incidenti stradali?".
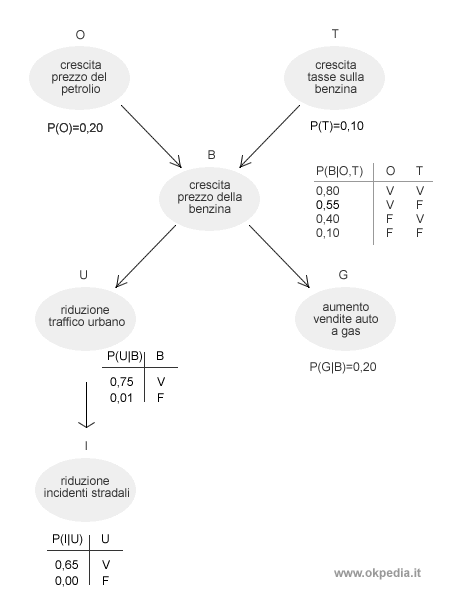
Il sistema è composto dalle seguenti variabili ( O, T, B, U, G, I ). La variabile O è una variabile di prova, poiché indica l'evento che condiziona la domanda, ossia l'incremento del prezzo del petrolio. La variabile O viene, pertanto, considerata come un valore costante uguale a V ( vero ).
Le variabili T, B, U, G, I sono le variabili nascoste e sono quelle che il sistema può modificare in ogni iterazione. La variabile I è anche la variabile obiettivo che è vera quando si riducono gli incidenti stradali
Per ipotesi la situazione di partenza (N=0) è la seguente:
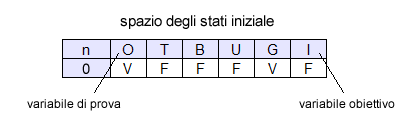
Nella prima iterazione l'algoritmo modifica la variabile T, lasciando invariate tutte le altre. Il nuovo valore da assegnare alla variabile T viene campionato in base alla sua catena di Markov, ossia il valore corrente dei nodi genitori, dei nodi figli e degli altri nodi genitori dei figli.
In questo caso il nodo T non ha nodi genitori, la sua probabilità di essere vero è P(T)=0,20. Il nodo T ha solo un nodo figlio B che ha come altro genitore il nodo O. Nello spazio corrente degli stati il nodo B è falso e l'altro nodo genitore O è vero. La probabilità del nodo figlio B di avere il valore corrente (falso) è 0,45, pari all'inverso di 0,55.
P(T) = 0,20 , P(B|O,T) = 0,45
L'algoritmo può calcolare la probabilità del nodo T moltiplicando la sua probabilità condizionata ai genitori con quella dei nodi figli.
P'(T) = P(T) P(B|O,T) = 0,20 · 0,45 = 0,09 = 9%
Data questa distribuzione probabilistica si ipotizza che l'algoritmo assegni alla variabile T il valore vero. Ora, lo spazio degli stati corrente è il seguente:
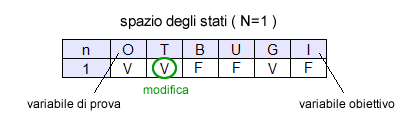
Questa nuova distribuzione dei valori consente di calcolare il nuovo valore della variabile obiettivo I che viene rilevato e registrato. In questo caso il valore della variabile I è vero.
Va specificato che l'algoritmo poteva anche confermare il valore già esistente del nodo. La variazione del suo valore è casuale ed è condizionata alla distribuzione probabilistica della sua catena di Markov. Tra i vari valori assegnabili dal dominio della variabile c'è anche il valore corrente del nodo.
L'algoritmo ora procede in altre tre iterazioni. In ogni iterazione modifica una sola variabile non di prova alla volta e rileva l'effetto sulla variabile obiettivo I.
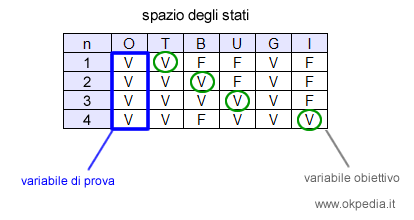
Al termine delle iterazioni, l'algoritmo conta quante volte la variabile obiettivo I è vera (Iv=1) e lo rapporta al numero delle iterazioni (N=4).
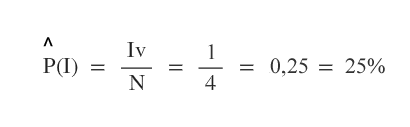
Ne consegue che, se il prezzo del petrolio aumenta, il numero degli incidenti si riduce una volta su quattro. Pertanto, la probabilità di una riduzione del numero degli incidenti è pari a 1/4 ossia al 25%.
L'algoritmo ha così risposto alla domanda iniziale.
La differenza tra campionamento diretto e MCMC
Queste tecniche si distinguono da quelle basate sul campionamento diretto, in quanto modificano soltanto il valore di una variabile alla volta, lasciando invariato quello di tutte le altre variabili non condizionate da quest'ultima. Nel campionamento diretto, invece, a ogni iterazione viene assegnato un valore random a tutte le variabili.
