Eliminazione strategie dominate
L'eliminazione delle strategie dominate è un'operazione preliminare della teoria dei giochi che consiste nell'eliminazione delle strategie con pay-off inferiore ( strategie dominate ) dalle combinazioni strategiche possibili del gioco, al fine di concentrare lo studio sulle strategie dominanti. In condizioni di razionalità perfetta, i giocatori scartano sempre le strategie dominate poiché sono caratterizzate da pay-off inferiori rispetto alle altre strategie alternative ( dominanti ).
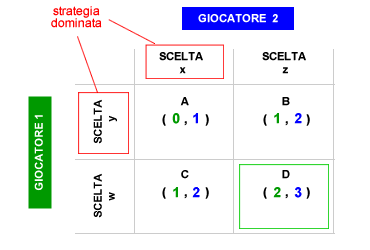
Ad esempio, nella matrice precedente il giocatore 1 ( verde ) può scegliere tra la strategia w e la strategia y. La strategia w consente al giocatore 1 di ottenere un pay-off compreso tra 0-1 ( A-B). La strategia y gli consente, invece, di ottenere un pay-off compreso tra 1-2 ( C-D). In condizioni di razionalità il giocatore 1 preferisce la strategia w alla strategia y poiché gli permette di sperare in un pay-off superiore ( 1-2 > 0-1 ). Lo stesso può dirsi per il giocatore 2, il quale preferisce la strategia z alla strategia x in quanto gli consente di ottenere un pay-off superiore ( 2-3 > 1-2 ). Le strategie y e x sono due strategie dominate. Il gioco ha un equilibrio stabile e ottimale nella cella D.
Efficienza. L'eliminazione delle strategie dominate consente di concentrare l'attenzione e lo studio del gioco soltanto sulle strategie migliori ( efficienza ). Ciò consente di individuare più rapidamente l'equilibrio strategico del gioco.
Assenza strategie dominate. Le strategie dominate sono situazioni rare in un gioco. Nella maggior parte dei giochi non vi sono strategie dominate da eliminare.
Dilemma del prigioniero. L'eliminazione delle strategie dominanti non assicura sempre il raggiungimento di un equilibrio ottimale. Al contrario, l'eliminazione delle strategie dominanti potrebbe anche portare al risultato peggiore per entrambi i giocatori o essere inefficace/inefficiente. Ad esempio, nel caso del dilemma del prigioniero la strategia di non confessare è la strategia dominata. Entrambi i giocatori scelgono di confessare ottenendo un leggero sconto di pena. Qui di seguito è rappresentata la matrice del "dilemma del prigioniero".
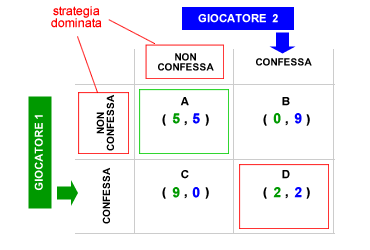
Nella matrice l'equilibrio del gioco ( D ) è il peggiore possibile per entrambi i giocatori. L'equilibrio ottimale ( A ) può essere raggiunto soltanto quando i due giocatori scelgono di non confessare ( strategia dominata ).Nella cella D l'utilità sociale è pari a 4 ( 2+2 ) mentre nella cella A l'utilità sociale è pari a 10 ( 5+5 ). Allo stesso modo, il pay-off individuale nella cella D è pari a 2 per entrambi i giocatori, mentre nella cella A il pay-off individuale dei giocatori è pari a 5. In conclusione, nel caso del dilemma del prigioniero l'eliminazione delle strategie dominate non conduce all'equilibrio ottimale del gioco bensì al peggiore equilibrio possibile sia dal punto di vista individuale ( pay-off individuale ) che sociale ( somma dei pay-off ).
- Eliminazione iterata delle strategie dominate. Nei giochi sequenziali le strategie dominate dei giocatori possono essere scartate al termine di ogni turno, poiché è razionale aspettarsi che non siano scelte dall'avversario. Se gli agenti sono razionali e hanno accesso a un'informazione completa del gioco, è possibile eliminare le strategie dominate dal gioco. Ogni giocatore può formarsi un'aspettativa sul comportamento razionale dell'altro e, quindi, scartare gradualmente le sue scelte di gioco peggiori tra quelle possibili. Ciò consente di ridurre la rappresentazione dell'albero di gioco. Non è comunque detto che l'eliminazione razionale delle strategie dominate conduca a un risultato di gioco ottimale.
