Concatenazione in avanti del primo ordine

La concatenazione in avanti del primo ordine è la tecnica della concatenazione in avanti applicata alle formule della logica del primo ordine. Le formule atomiche della base di conoscenza sono elaborate con il Modus Ponens per aggiungere nuove formule atomica alla base di conoscenza. A partire dalle premesse inziali il processo di inferenza deduce nuove formule e nuovi fatti per unificazione delle premesse. Il seguente schema rappresenta il processo deduttivo di inferenza in un albero logico che viene elaborato dall'alto ( premesse ) verso il basso ( conclusione ). Ogni livello di profondità dell'albero di ricerca rappresenta un'iterazione.

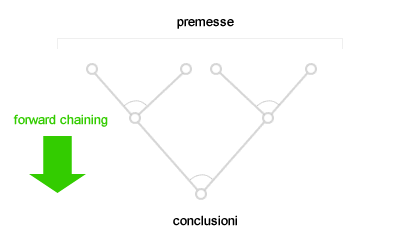
Durante ogni iterazione i nuovi fatti sono aggiunti alla base di conoscenza per essere elaborati nell'iterazione successiva come fatti noti. La combinazione dei nuovi fatti con quelli noti produce altri fatti nuovi e così via. Il processo di inferenza in avanti dell'algoritmo si conclude quando non è possibile aggiungere nuove formule a partire da quelle esistenti. Quando si verifica questa situazione finale, la base di conoscenza raggiunge il suo punto fisso ( punto fisso della base di conoscenza ) e nessun'altra conseguenza logica può essere inferita.

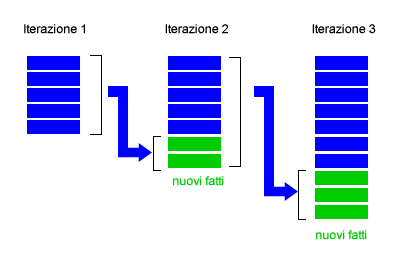
Per comprendere il funzionamento dell'algoritmo della concatenazione in avanti del primo ordine è consigliabile utilizzare un esempio pratico. Nel seguente esempio viene trasformata una frase dal linguaggio naturale alla logica del primo ordine e aggiunta a una base di conoscenza. La base di conoscenza iniziale è composta da cinque formule.

Qualsiasi algoritmo di ricerca del primo grado potrebbe rispondere a domande come le seguenti: "Cosa possiede Tizio?", "Tizio è minorenne?", ecc. La base di conoscenza non è però completa poiché diversi nuovi fatti potrebbero essere dedotti e aggiunti alla base dati. Il processo inferenziale tramite la concatenazione in avanti consente di individuare le nuove deduzioni applicando il metodo dell'unificazione delle formule.

La concatenazione iniziale ha inferito altri quattro fatti semplicemente applicando il metodo del Modus Ponens ai fatti già conosciuti. Dopo ogni nuova scoperta l'algoritmo rianalizza tutte le combinazioni delle formule alla ricerca di nuovi fatti deducibili. Il processo termina quando nessun nuovo fatto emerge dalla comparazione delle formule, in questo caso la base di conoscenza giunge al suo punto fisso e il processo di inferenza si conclude. Al termine del processo di inferenza la base di conoscenza ha ampliato la propria dimensione dalle cinque formule iniziali alle nove formule finali. L'algoritmo di ricerca può, quindi, rispondere a nuove domande come "è illegale l'attività di Caio?", "Caio vende alcolici?", "Tizio possiede alcolici?", ecc. Tutte le conseguenze logiche sono incluse nella base di conoscenza.

---

• Differenza tra la concatenazione in avanti della logica proposizionale e quella del primo ordine. Il principio di funzionamento della concatenzione in avanti del primo ordine è simile a quello della concatenzione in avanti della logica proposizionale. Tuttavia, mentre nella logica proposizionale le clausole sono caratterizzate da valori booleani ( vero o falso ), le formule della base di conoscenza nella logica del primo ordine sono, invece, dei predicati caratterizzati da variabili ( es. x, y, z ).
• Completezza. La concatenazione in avanti in una base di conoscenza del primo ordine è completa, dopo aver raggiunto il proprio punto fisso, poiché consente di rispondere a tutte le interrogazioni ( query ) possibili, sulla base delle premesse ( fatti noti ) e delle conseguenze logiche deducibili. L'algoritmo inferenziale è completo se il problema è composto soltanto da formule e da costanti ed è privo di funzioni, in quanto dopo n iterazioni l'algoritmo giunge al punto fisso della base di conoscenza.
  
  
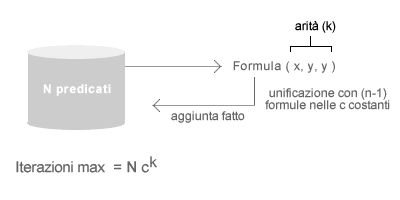
  La base di conoscenza iniziale dell'esempio precedente ha un'arità pari a tre ( k=3 ), in quanto il numero massimo degli argomenti ( x, y, z ) di una formula è uguale a tre. La base di conoscenza è composta da cinque predicati ( N=5 ) e da tre simboli di costante ( c=3 ) che sono i seguenti: "Tizio", "Caio", "vodka". L'algoritmo inferenziale impiega al massimo Nc^k iterazioni per giungere al punto fisso, ossia 5· 3³ iterzioni ( 45 iterazioni ).
• Pattern matching inefficiente. L'algoritmo della concatenazione in avanti compara le formule atomiche della base di conoscenza con tutte le altre formule e su tutti gli argomenti ( pattern matching ). Al termine di un'interazione, il processo di ricerca inferenziale riparte dall'inizio su tutte le formule ( originarie e aggiunte ), in modo tale da poter verificare nuove conseguenze logiche dall'unificazione delle premesse con l'ultimo fatto aggiunto, e così via.
  
  
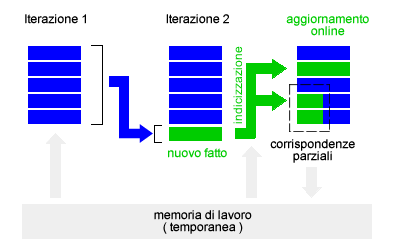
  Questo processo è efficace e completo ma anche molto inefficiente, poiché implica un elevato tempo di esecuzione dell'algoritmo e una grande quantità di spazio di memoria. Il pattern matching elabora tutti le conseguenze logiche e, quindi, anche quelle che potrebbero non essere utili al processo di ricerca, fatti inutili, dettagli irrilevanti o di poca importanza. Una possibile soluzione del problema è l'algoritmo della concatenazione all'indietro che, partendo dagli obiettivi, lavora soltanto sui fatti più rilevanti.
• Aggiornamento online. L'aggiornamento online è una variante del processo inferenziale. Quando il processo inferenziale scopre un nuovo fatto, grazie a un'opportuna indicizzazione può individuare tutti gli altri fatti della base di conoscenza che sono influenzati dalla scoperta e li aggiorna. Il processo di aggiornamento online continua a cascata in avanti fino al raggiungimento di un punto fisso. Quando il processo di aggiornamento online giunge al punto fisso, nessun nuovo fatto può essere modificato o inferito, l'algoritmo passa ad analizzare il fatto successivo.
  
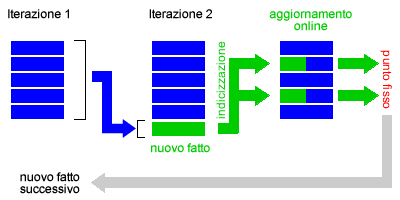
• Memoria di lavoro e corrispondenze parziali. Il processo inferenziale di aggiornamento può generare corrispondenze complete ( nuovi fatti ) e corrispondenze parziali. Le corrispondenze parziali sono formule i cui congiunti non sono ancora tutti noti. Ad esempio, una corrispondenza parziale è la formula Vendere(Tizio, y, Caio) in cui sappiamo che Tizio sta vendendo qualcosa a Caio ma non sappiamo ancora cosa ( variabile y ). Per evitare di dover ricalcolare ogni volta le corrispondenze parziali è consigliabile memorizzarle in una memoria di lavoro temporanea, in modo tale da prelevarle aggiornate nelle successive iterazioni.
  
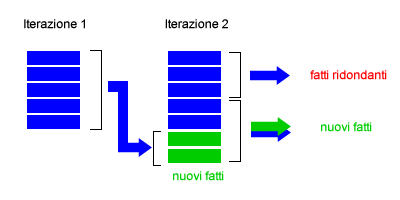
• Matching ridondante. A ogni iterazione l'algoritmo produce nuovi fatti ( formule ) che si aggiungono a quelli già presenti nella base di conoscenza. Per evitare la produzione di fatti ridondanti, nell'iterazione t è consigliabile vincolare la produzione/aggiunta dei nuovi fatti soltanto quando la formula utilizza come argomento almeno un fatto scoperto nell'iterazione precedente (t-1). In questo modo soltanto le conseguenze logiche che derivano dalle ultime deduzioni sono prese in considerazione. Le conseguenze logiche che non hanno nemmeno un fatto scoperto nell'iterazione precedente (t-1) possono essere scartate, poiché sono evidentemente ridondanti, in quanto sono state sicuramente aggiunte nelle iterazioni precedenti. Questa modifica migliora notevolmente l'efficienza computazionale dell'algoritmo di concatenazione in avanti di primo ordine.
  
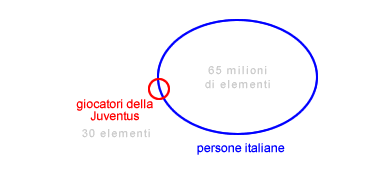
• Ordinamento dei congiunti. Anche l'ordine di scelta degli argomenti potrebbe influire notevolmente sul tempo di esecuzione dell'algoritmo. Quando ci sono due o più percorsi per giungere a uno stesso obiettivo, è preferibile selezionare come primo argomento sempre quello con minor numero di elementi. Ad esempio, per verificare quanti giocatori italiani giocano nella Juventus, potremmo selezionare tutte le persone italiane nel mondo ( 65 milioni ) e verificare se giocano nella Juventus. È però ovvio che sarebbe meglio selezionare prima i giocatori della Juventus, una trentina al massimo, e verificare quanti di questi hanno la cittadinanza italiana. L'esempio può sembrare banale ma rende bene l'idea del problema della scelta degli argomenti di ricerca.
  
  
• Funzioni e incompletezza. La presenza di una o più funzioni nelle formule della base di conoscenza del primo ordine può rendere incompleto il processo di inferenza e di ricerca. Se una funzione ha infiniti argomenti ( es. numeri naturali ) ha anche infinite conclusioni logiche. In questo caso il processo di ricerca inferenziale non giunge mai a un punto fisso e il tempo di esecuzione dell'algoritmo è infinito. La presenza delle funzioni rende la base di conoscenza incompleta. Per evitare il loop infinito è possibile configurare un valore di taglio ( t=1G ) alle iterazioni, oltrepassato il quale l'algoritmo interrompe l'esecuzione. Tuttavia, quando l'algoritmo inferenziale non giunge a una soluzione entro un miliardo di iterazioni ( 1G iter. ), nessuno può affermare con certezza che il problema non abbia soluzione poiché quest'ultima potrebbe essere teoricamente situata nella successiva iterazione ( 1G+1 iter. ). In conclusione, la base di conoscenza è incompleta e il problema della logica del primo ordine è semidecidibile. La presenza delle funzioni introduce un problema di incertezza nel quadro logico della rappresentazione della realtà.