Regole di conversione in CNF ( logica del primo ordine )
La conversione dalla logica del primo ordine al CNF ( forma normale congiuntiva ) consente di rappresentare le formule logiche in una forma più semplificata e computabile per gli agenti razionali ( algoritmi ). La rappresentazione delle formule nella forma CNF è inferenzialmente equivalente a quella della logica del primo ordine. Le principali tecniche e/o operazioni per convertire una formula dalla logica del primo ordine alla forma CNF sono le seguenti:
- Eliminazione delle implicazioni. Le implicazioni logiche sono trasformate in una disgiunzione di letterali, ove la premessa si presenta nella sua forma negata. Ad esempio, l'implicazione Gatto(x)⇒Mammifero(x) viene trasformata in ¬ Gatto(x) ∨ Mammifero(x).
- Eliminazione dei quantificatori esistenziali. Nella logica del primo ordine sono utilizzati i quantificatori esistenziali ( E ). È possibile eliminare i quantificatori esistenziali trasformandoli in quantificatori universali ( V ) oppure ricorrendo all'utilizzazione delle costanti di Skolem ( skolemizzazione ).
- Trasformazione dei quantificatori. Nella logica del primo ordine i quantificatori esistenziali possono essere trasformati in quantificatori universali e viceversa. La seguente tabella mostra le principali regole di trasformazione applicabili sui quantificatori negati.
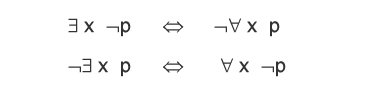
- Istanziazione esistenziale ( costanti ). L'istanziazione esistenziale consiste nella sostituzione di un quantificatore esistenziale ( ∃ ) con l'utilizzo di una costante che la risolve. Ad esempio, scrivere "esiste almeno un valore di x che rende vera l'espressione P" ( ∃ x P(x) ) può essere trasformata in P(A) dove A è il nome della nuova costante (x=A) che rende vero il quantificatore esistenziale.
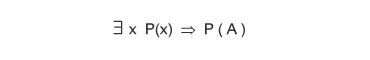
Funzioni di Skolem. Le funzioni di Skolem sono utilizzate nella forma normale congiuntiva ( CNF ) del primo ordine per indicare le variabili quantificate all'interno delle formule logiche. La variabile x viene sostituita con un quantificatore esistenziale ( costante di Skolem ) che soddisfa il letterale. Ciò consente di utilizzare l'istanziazione esistenziale su più costanti all'interno di un unico quantificatore esistenziale. Ad esempio, nella seguente formula le funzioni di Skolem sono A(x) e B(x). Ogni funzione di Skolem indica un argomento diverso della variabile x. La prima formula utilizza soltanto una sola funzione di Skolem e assume un significato logico completamente diverso rispetto alla seconda formula che ha due funzioni di Skolem.
- Trasformazione dei quantificatori. Nella logica del primo ordine i quantificatori esistenziali possono essere trasformati in quantificatori universali e viceversa. La seguente tabella mostra le principali regole di trasformazione applicabili sui quantificatori negati.
- Nomi delle variabili. Nelle funzioni e nei quantificatori della logica del prime ordine è necessario utilizzare diversi nomi per le variabili per evitare confusione. Ad esempio, scrivere ∀x P(x) ∧ ∃ x Q(x) è ambiguo in quanto può creare confusione.
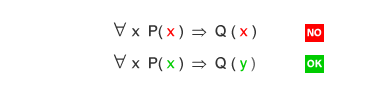
- Quantificatore universale. Il quantificatore universale può essere eliminato nella forma CNF in quanto è implicito. Scrivere ∀ x P(X) equivale a scrivere P(x).
- Distribuzione delle disgiunzioni. Per giungere alla forma CNF finale potrebbe essere necessario modificare la distribuzione per raggruppare le disgiunzioni annidate ( ∨ ) rispetto alle congiunzioni ( ∧ ) in modo tale da ottenere una sequenza di clausole. Ad esempio, la formula ( A ∧ B ) ∨ C può essere espressa nella forma CNF come ( A ∨ C ) ∧ ( B ∨ C ).
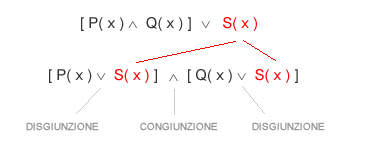
Le regole di conversione consentono di ottenere una formula logica del primo ordine nella forma normale congiuntiva ( CNF ). Nella forma CNF la formula è composta da una serie di congiunzioni ( ∧ ) e disgiunzioni annidate ( ∨ ).
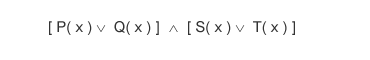
Computabilità della forma CNF. La rappresentazione nella forma CNF consente di elaborare la formula logica in un algoritmo. La formula del primo ordine nella forma CNF non è immediatamente comprensibile agli occhi di un essere umano ma è più facilmente computabile da un algoritmo.
- Dimostrazioni per assurdo. Quando la forma CNF non è logicamente soddisfacibile, allora nemmeno la forma originale nella logica del primo ordine non è soddisfacibile. Ciò consente di utilizzare la forma CNF per eseguire le dimostrazioni per assurdo.
