Come rappresentare i dati statistici
La rappresentazione dei dati statistici deve essere costruita in modo tale da agevolare la lettura e l'interpretazione delle informazioni. Non è sempre facile e, spesso, è il risultato di una serie di scelte soggettive del ricercatore. In questo tutorial si vedrà come costruire una rappresentazione per classi a partire dai dati grezzi raccolti con una rilevazione statistica.
Un esempio pratico di rappresentazione
Facciamo un esempio pratico, in una sessione di esame di statistica si presentano 39 studenti universitari. Dopo qualche giorno, i voti dei compiti sono pubblicati sulla bacheca del dipartimento di statistica dell'Università sotto la forma di un elenco di nomi e di voti.
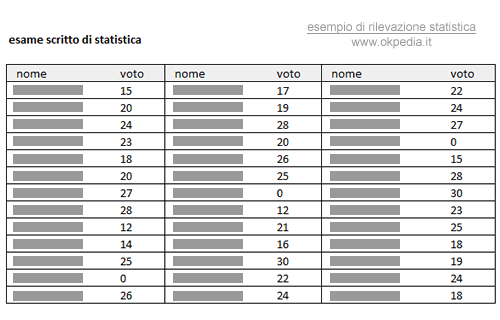
Questo elenco è il dato grezzo della rilevazione statistica. Si tratta di un'informazione completa, utile per trovare il proprio voto all'esame, ma poco utile per capire il fenomeno statistico nella sua complessità.
Potremmo fare una media aritmetica dei voti ma, se il fenomeno è molto complesso, rischieremmo di perdere informazioni o addirittura di avere un'informazione fuorviante.
Ad esempio, la media aritmetica dei voti nella tabella precedente è pari a 20,1. Gli studenti sono andati in media più bene o male? Non lo sappiamo ancora.

Dal voto medio emerge però una prima interpretzione. La media del venti ci semba bassa e induce a pensare che gli studenti siano andati male. Come vedremo, la realtà è molto diversa se approfondiamo l'analisi statistica dei dati.
La distribuzione delle frequenze
Per rappresentare meglio la variabile statistica, elenchiamo in ordine crescente tutti i voti da 0 a 30 ( le modalità ) e contiamo per ciascuno di essi il numero di volte che si presenta ( la frequenza assoluta ). In questo modo, otteniamo la distribuzione delle frequenze assolute.
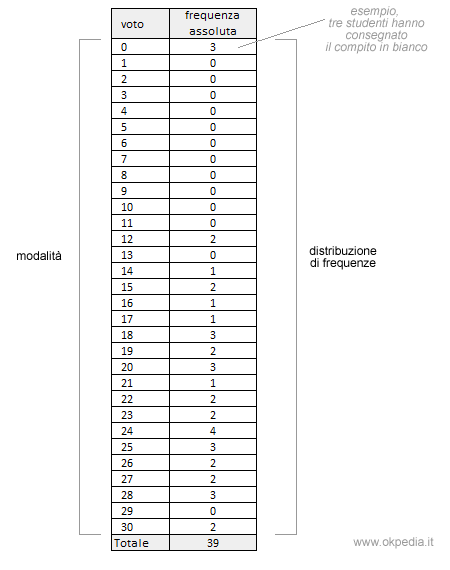
La rappresentazione può essere ulteriormente migliorata indicando le frequenze relative di ciascun dato in valori percentuali. Sommiamo tutte le frequenze assolute e indichiamo il totale nella riga finale della colonna.
Per calcolare la frequenza relativa di ciascuna modalità, dividiamo la sua frequenza assoluta per il totale delle frequenze assolute. Infine, moltiplichiamo il quoziente per cento, e otteniamo la frequenza relativa in percentuale.
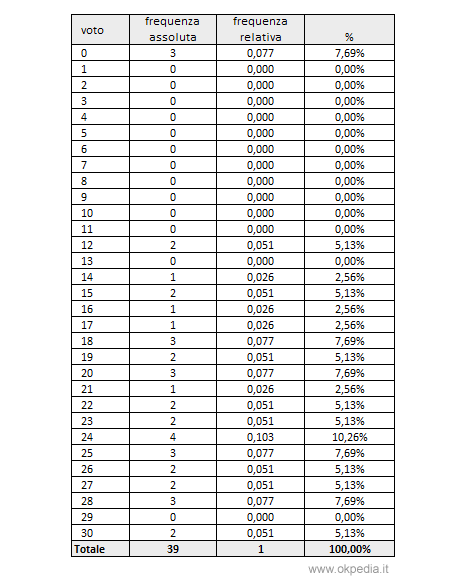
E' importante sommare anche le frequenze relative e indicare il totale nella riga finale. Se tutto è corretto, la somma delle frequenze relative è pari a uno (1), quella delle frequenze relative percentuali è pari a cento (100%).
Questa informazione sintetica è completa ma poco leggibile poiché non ci consente di capire a colpo d'occhio l'andamento generale dell'esame. Dobbiamo sintetizzare ulteriormente i dati.
Per semplificare l'interpretazione dei dati dobbiamo introdurre l'uso delle classi di frequenza. In altri termini, dobbiamo raggruppare le diverse modalità e sommare le loro frequenze assolute. La distribuzione per classi di frequenza rende più leggibile la rappresentazione e l'interpretazione delle informazioni contenute nei dati statistici.
Come fare la distribuzione per classi di frequenza
Il primo passo consiste nel trovare il valore minimo e il valore massimo della modalità che stiamo studiando ( il voto di esame ). In questo caso, il valore più basso è zero (0), quello più alto è trenta (30).

La differenza tra il valore massimo e il valore minimo ci permette di calcolare il campo di variazione del fenomeno statistico. In questo caso, il campo di variazione è pari a trenta ( 30-0=30 ).
Dividiamo il campo di variazione per un numero di classi. Le classi di frequenze sono dei raggruppamenti di due o più modalità. Ad esempio, la classe 18-22 comprende tutti i voti da 18 a 22.
Quante classi di frequenza utilizzare
Il numero delle classi è determinato dai gradi informativi, ogni classe deve veicolare un'informazione differente dalle altre. Il numero delle classi non deve essere né troppo basso, né troppo alto.
- Se il numero delle classi è troppo basso, si rischia d'essere troppo sintetici e non rappresentare bene la complessità del fenomeno.
- Se il numero delle classi è troppo alto, la rappresentazione potrebbe non essere facilmente interpretabile, rendendo difficoltoso trovare l'informazione rilevante. Come si vedrà più avanti, a volte questa tecnica inefficace potrebbe essere appositamente adottata dai ricercatori per nascondere alcune informazioni.
In questo caso, ci interessa rappresentare bene l'informazione. Dobbiamo trovare le informazioni più rilevanti e significative per rappresentare bene il fenomeno. Qui di seguito sono presenti alcune classi, individuate secondo un metodo di ripartizione soggettivo, e a ciascuna classe abbiamo associato un significato.
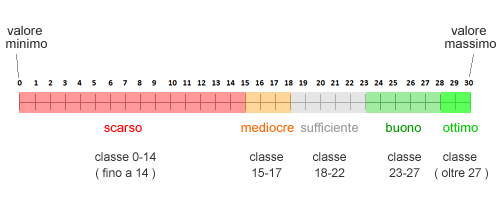
- Fino a quattordici ( "scarso" ). I voti fino a 14 sono troppo bassi. In genere, se l'esame universitario è suddiviso in scritto e orale, un voto fino a quattordici non consente di accedere all'esame orale. Possiamo, quindi, raggruppare tutti questi voti in un'unica categoria poiché trasmettono la medesima informazione. Possiamo anche dare un nome a questa categoria: "scarso". La classe ha un'ampiezza pari a quindici poiché comprende i valori da 0 a 14.
- Da quindici a diciassette ( "mediocre" ). I voti da 15 a 17 sono bassi, indicano una preparazione mediocre ma non scarsa. Chi consegue questi voti può sperare di ottenere la sufficienza all'esame orale. Non è completamente impreparato ma nemmeno sufficientemente preparato. Anche in questo caso, la classe trasmette un'informazione precisa e distinta dalle altre classi, e può essere associata alla preparazione "mediocre". La classe ha un'ampiezza pari a tre poiché comprende i voti 15, 16 e 17.
- Da diciotto a ventidue ( "sufficiente" ). I voti da 18 a 22 indicano una preparazione appena sufficiente sull'argomento. Questa classe identifica un'altra informazione significativa e può essere associata alla preparazione "sufficiente". È quindi un'altra classe utile per la nostra rappresentazione. La classe ha un'ampiezza pari a cinque, poiché comprende i voti da 18 a 22.
- Da ventitre a ventisette ( "buono" ). I voto da 23 a 27 sono conseguiti dagli studenti con una buona preparazione sulla materia. Questi studenti hanno un grado di conoscenza superiore rispetto a quelli della classe precedente ma non è ancora ottimale. Questa informazione è significativa per l'interpretazione dei dati e può essere raggruppata in una classe specifica e a una categoria qualitativa ( "buono" ). La classe ha un'ampiezza pari a cinque, poiché comprende i valori 23, 24, 25, 26 e 27.
- Oltre ventisette ( "ottimo" ). Quest'ultimo raggruppamento comprende i voti compresi da 28 a 30. Sono studenti che hanno dimostrato di possedere una conoscenza ottimale della materia. È consigliabile separarli dalla classe precedente e dedicare loro una classe specifica ( oltre 27 ) e una categoria qualitativa ad hoc ( "ottimo" ). La classe ha un'ampiezza pari a tre poichè comprende i valori 28, 29 e 30.
Abbiamo individuato cinque classi e ogni classe ha un significato preciso, inequivocabile e distinto rispetto alle altre. Nella ripartizione non è importante che ogni classe comprenda lo stesso numero di valori ( l'ampiezza della classe ), ciò che conta è che sia significativa.
La rappresentazione per classi di frequenza dei dati statistici
Proviamo a rappresentare la distribuzione per classi di frequenza in una tabella. Per ciascuna classe di frequenza contiamo il numero dei voti che cadono nell'intervallo. Questo ci consente di ottenere le frequenze assolute di ciascuna classe. Allo stesso modo, possiamo calcolare le frequenze relative e quelle percentuali delle classi. Il risultato finale è il seguente:
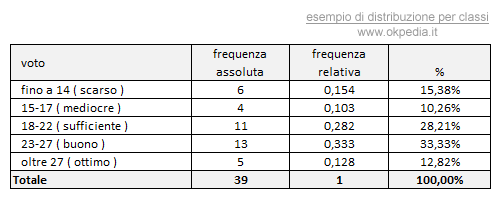
Come si può notare, la distribuzione per classi è una rappresentazione molto più efficace. È molto più semplice interpretare l'informazione nei dati, in quanto il numero delle modalità si è ridotto da trenta a cinque, ed è facile da leggere. Ogni classe veicola un significato e un'informazione ben precisa.
E' sufficiente un colpo d'occhio alla tabella per capire subito che gli studenti sono andati bene all'esame. Soltanto il 25% è sotto la sufficienza. Il 46% degli studenti ha conseguito un risultato tra buono e ottimo. Il 28% ha strappato la sufficienza. Tutto sommato, è un buon risultato.
In conclusione
La rappresentazione per classi ci ha permesso di comunicare meglio l'informazione contenuta nei dati. Non esiste però un metodo oggettivo di scelta delle classi, molto però dipende dalla costruzione e dalla scelta delle modalità. Si tratta perlopiù di scelte soggettive del ricercatore. Questa tecnica può essere utile per rappresentare meglio l'informazione, così come abbiamo dimostrato in questa pagina, ma può essere anche utilizzata per enfatizzare di più alcuni significati e occultarne altri.
La scelta delle classi e l'interpretazione dei dati
La suddivisione in classi è una scelta soggettiva del ricercatore e può influenzare sensibilmente l'interpretazione dei dati. Ad esempio, dalla seguente tabella spicca la classe di maggioranza degli studenti che hanno ottenuto un buon risultato alla sessione di esame (33,3%).

Il lettore interpreta la tabella in un certo modo, viene soprattutto colpito dl fatto che la maggioranza degli studenti abbia dimostrato di possedere una buona preparazione sulla materia.
Proviamo ora a modificare le classi, accorpando in un'unica classe tutti i giudizi al di sotto di buono ( scarso + mediocre + sufficiente ) e lasciando separate le classi dei voti più alti.
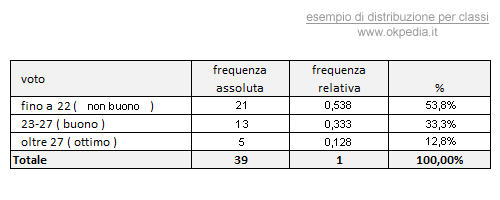
La nuova distribuzione delle classi enfatizza il peso dei voti bassi ( 53,8% ). Questa volta il lettore viene colpito dalla percentuale più alta della prima classe, quella dei voti non buoni, e interpreta il dato come una scarsa preparazione degli studenti.
Come si può notare, quest'ultima interpretazione è esattamente opposta alla precedente, pur essendo tratta dagli stessi dati statistici. Ciò che cambia è la rappresentazione dei dati.
In conclusione, modificando la distribuzione e l'ampiezza delle classi, si può influenzare l'interpretazione dei dati e il significato dell'analisi statistica.
