La classe di frequenze
Nell'analisi statistica univariata una classe è un intervallo di una modalità di un carattere quantitativo. È un insieme compreso tra un valore minimo ( estremo inferiore della classe ) e un valore massimo ( estremo superiore della classe ).
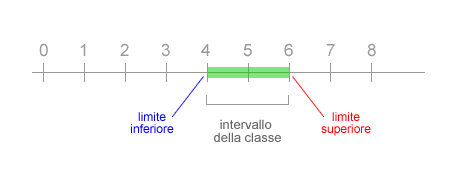
Una classe è una parte del campo di variazione della distribuzione di frequenze. Le classi sono utilizzate nelle modalità quantitative per agevolare l'interpretazione delle informazioni dai dati. Possono essere chiuse o aperte e, a seconda dei casi, sono elencate secondo un ordine crescente o decrescente.
Un esempio di classi di frequenze
Ad esempio, in un esame il voto è la variabile statistica che può assumere come modalità i valori compresi tra 0 e 10. Data una popolazione statistica di 20 studenti, i voti dell'esame possono essere rappresentati in modo sintetico tramite la distribuzione delle frequenze.
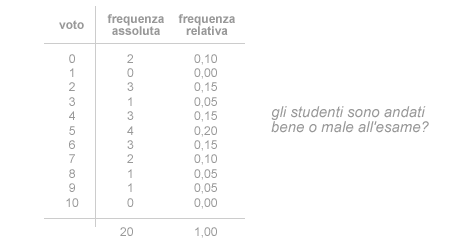
Questa rappresentazione non ci consente di capire subito l'informazione. Non è facile capire, a colpo d'occhio, se gli studenti siano andati mediamente bene o male all'esame.
La precedente distribuzione delle frequenze può essere ulteriormente sintetizzata tramite l'ausilio delle classi di frequenze. Le classi sono una ripartizione del campo di variazione della distribuzione che semplifica l'interpretazione dei dati.
Nella seguente tabella sono presenti soltanto quattro classi. Una prima classe comprende i voti da 0 a 3, una seconda classe quelli da 4 a 5, una terza classe quelli da 6 a 7, e una quarta classe da 8 a 10.
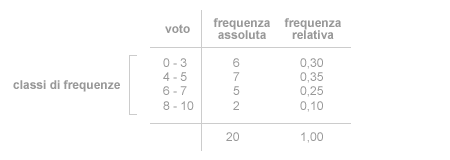
Le classi permettono di raggruppare i valori delle modalità aventi un significato simile. Gli studenti con un voto inferiore a 4 sono decisamente impreparati, indipendentemente dal fatto che prendano 2 o 3. Quelli che prendono 4 o 5, invece, hanno maggiori probabilità di recuperare il voto.
Le classi possono essere utilizzate per indicare delle categorie per veicolare meglio l'informazione. Ad esempio, la categoria degli studenti impreparati ( 0-3 ), degli studenti mediocri ( 4-5 ), degli studenti con la sufficienza ( 6-7 ) e di quelli con un'ottima preparazione ( 8-10 ).

La nuova rappresentazione espone l'informazione in modo più facilmente interpretabile, poiché le categorie sono soltanto quattro, contro le dieci modalità iniziali, e ogni categoria è associata un'informazione molto più rilevante ( scarso, mediocre, sufficiente, ottimo ) per l'osservazione del fenomeno.
Ad esempio, nella tabella precedente l'informazione rilevante è subito evidente a colpo d'occhio, gli studenti non sono andati bene all'esame. Il 65% degli studenti non ha raggiunto la sufficienza e soltanto il 10% ha dimostrato una preparazione ottimale.
Il limite e l'intervallo della classe
L'estremo inferiore e superiore di ogni classe è detto limite della classe. Tutti i valori compresi all'interno di una classe sono, invece, detti intervallo della classe. L'intervallo della classe può essere chiuso o aperto:
- Intervallo chiuso della classe. Sono indicati sia il limite minimo che il limite massimo della classe. Ad esempio, la classe 4-6 è un intervallo chiuso poiché è presente sia l'estremo inferiore (4) che l'estremo superiore (6).
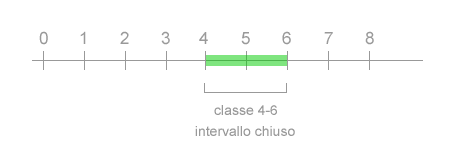
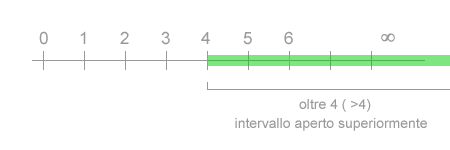
- Intervallo aperto della classe. Negli intervalli aperti è indicato soltanto un estremo, inferiore o superiore, mentre l'altro non è indicato. Ad esempio la classe "fino a 3" è un intervallo aperto inferiormente, poiché è indicato soltanto il limite superiore. La classe "oltre 4" è un intervallo aperto superiormente, poiché è fissato soltanto il limite inferiore (4) ma non quello superiore ( infinito ).
Nel caso delle classi successive con un limite in comune, per convenzione il limite si considera incluso nella classe successiva. Ad esempio, le seguenti due classi hanno il valore quattro in comune. Nella prima il quattro indica il limite superiore mentre nella seconda il limite inferiore.
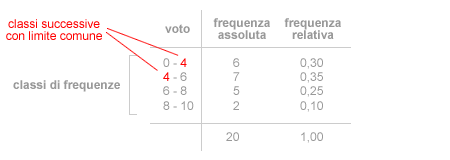
In questo caso, il valore quattro è considerato incluso nella seconda classe ( classe successiva ). Nella prima classe sono incusi tutti i valori fino a quattro ( escluso ). Nella seconda classe da quattro ( incluso ) a sei. E così via.
Per considerare sia il limite inferiore che il limite superiore appartenenti alla stessa classe, è necessario utilizzare un apposito simbolo di separazione, un trattino orizzontale chiuso ad entrambi i lati mediante due rette verticali.

La chiusura soltanto a destra indica la presenza di un intervallo chiuso con un estremo superiore incluso nella classe. La chiusura soltanto a sinistra, invece, indica un intervallo chiuso con l'estremo inferiore incluso nella classe. La parte priva di chiusura è da considerarsi sempre un intervallo chiuso ma, in questo caso, il limite non è compreso nella classe.
Il confine della classe
I confini della classe sono i limiti reali della classe quando si deve ricorrere all'arrotondamento dei valori. Ad esempio, la classe 4 |-| 6 ha un intervallo compreso tra il limite inferiore quattro (incluso) e il limite superiore sei ( incluso ). Entrambi i limiti sono numeri interi.
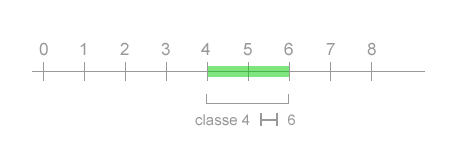
In presenza di dati decimali si potrebbe stabilire un arrotondamento del valore, a quello inferiore fino a 0.5 ( escluso ) oppure a quello superiore se oltre. Ad esempio, il valore 3.7 viene arrotondato a quattro (4) mentre il valore 6.2 viene arrotondato a sei (6).
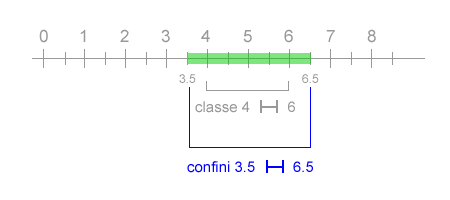
In questi casi, i limiti della classe non coincidono più ai limiti reali dell'intervallo. Nell'esempio precedente i valori 3.5 e 6.5 sono i confini della classe ossia i suoi limiti reali, inferiore e superiore.
L'ampiezza della classe
L'ampiezza di una classe è la differenza tra il limite superiore e inferiore della classe. Nei casi in cui ci sia l'arrotondamento dei dati ( es. da 2,7 viene considerato 3,0 ) l'ampiezza è la differenza tra i confini superiore e inferiore della classe. Ad esempio, nella seguente rappresentazione la classe è di ampiezza pari a due ( 6-4=2 )

Il valore centrale delle classi
In alcuni casi potrebbe essere utile indicate la classe con un valore centrale, calcolando la media aritmetica tra il limite inferiore e il limite superiore. Ad esempio, in sostituzione della classe 4-6 si può indicare il valore centrale 5.
- Come scegliere gli intervalli delle classi? È consigliabile scegliere degli intervalli che diano un significato all'intervallo della classe. Ad esempio, in un compito di scuola l'intervallo 4-5 è associato all'insufficienza. Se l'intervallo fosse più ampio, ad esempio 4-6, non veicolerebbe altrettanto bene l'informazione, poiché insieme ai compiti insufficienti, da 4 a 5, sono compresi anche quelli che l'hanno raggiunta (6). L'ampiezza ideale delle classi è determinata dalle caratteristiche dell'informazione.
- Cos'è il campo di variazione della distribuzione? E' l'intervallo della distribuzione di frequenze compreso dal valore minimo al valore massimo dei dati grezzi.
