La frequenza assoluta e relativa
In statistica la frequenza è un numero che sintetizza la distribuzione delle modalità di una variabile statistica. A partire di dati grezzi, acquisiti nella fase di rilevazione statistica, le frequenze consentono di rappresentare in modo sintetico le statistiche fondamentali del fenomeno.

Il ricercatore associa ogni modalità rilevante della variabile statistica al numero di volte ( frequenza ) in cui si presenta.
Nell'esempio precedente, la variabile statistica è l'esito del lancio della moneta e le modalità sono soltanto due ( testa o croce ). I dati grezzi possono essere riassunti in modo sintetico, associando a ciascuna modalità la frequenza con cui si è presentata durante la rilevazione.
Tipi di frequenze: assolute o relative
La frequenza è un dato sintetico e può essere assoluta o relativa.
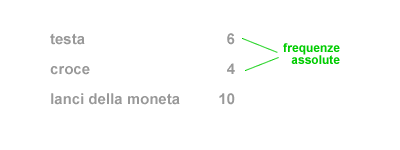
- Frequenza assoluta. La frequenza assoluta di un fenomeno è il numero intero di volte che questo si present durante una rilevazione statistica. Ad esempio, lanciando dieci volte una moneta, il lato "testa" della moneta si presenta sei volte. Il numero sei è la frequenza assoluta del fenomeno ( "testa" ).
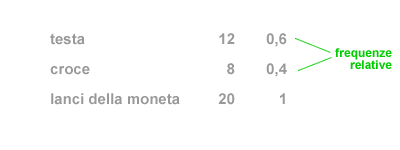
- Frequenza relativa. La frequenza relativa di un fenomeno è il rapporto tra la frequenza assoluta dello stesso e il numero totale dei casi esaminati nella rilevazione statistica. Ad esempio, dopo aver lanciato dieci volte la moneta, il lato testa si presenta con una frequenza relativa pari a 0,6 ossia nel 60% dei casi.
- Frequenza relativa percentuale. Le frequenze relative percentuali sono il prodotto della moltiplicazione per cento delle frequenze relative. Sono anche dette semplicemente percentuali. Le percentuali sono molto utilizzate nella vita quotidiana e rendono più semplice la rappresentazione statistica dei dati.

La distribuzione della frequenza
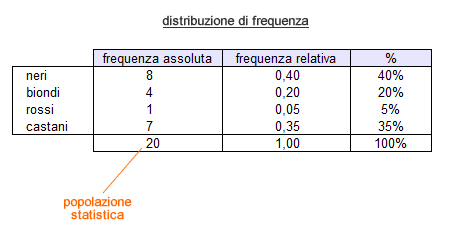
La distribuzione delle frequenze di una variabile statistica è rappresentata tramite una tabella. Nella prima colonna della tabella sono indicate le modalità della variabile. Nella seconda colonna sono rappresentate le frequenze assolute e/o le frequenze relative delle stesse.
L'uso delle frequenze in un'indagine statistica permette la rappresentazione dei dati statistici in una forma sintetica. La rappresentazione sintetica dei dati agevola l'interpretazione dei risultati dell'indagine statistiche che altrimenti sarebbe molto difficoltosa da effettuare tramite un'analisi dei dati grezzi.
Le frequenze cumulate e retrocumulate
Le frequenze assolute cumulate sono la somma delle frequenze assolute che si succedono dalla prima all'ultima classe in una distribuzione di frequenze. Ad esempio, la frequenza cumulata assoluta della seconda classe è pari alla somma delle frequenze assolute della prima e della seconda classe, e cosi via.
Dividendo le frequenze cumulate assolute per il il totale, si possono calcolare le frequenze cumulate relative. Moltiplicando per cento le frequenze cumulate relative, è possibile ottenere anche le frequenze cumulate percentuali.
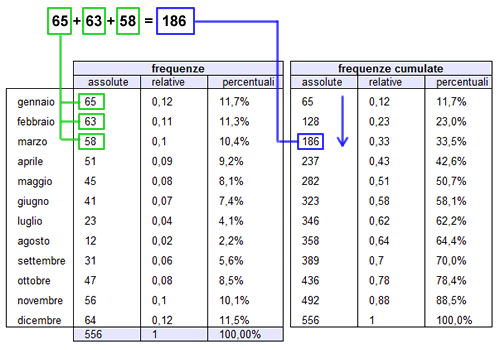
La distribuzione frequenza cumulata, relativa o assoluta, diventa significativa e veicola un'informazione a se stante. Ad esempio, ci consente di capire a colpo d'occhio l'andamento delle vendite nel corso dell'anno e individuare le fluttuazioni stagionali, o altre informazioni utili per l'analisi statistica.
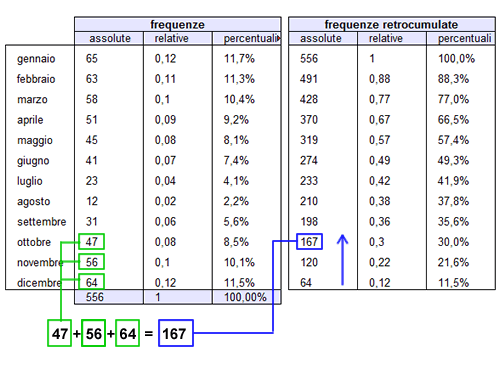
In modo speculare, si possono calcolare le frequenze retrocumulate assolute, relative o percentuali, sommando le frequenze a partire dall'ultima classe fino alla prima. In quest'ultimo caso la somma delle frequenze si svolge dal basso verso l'alto.
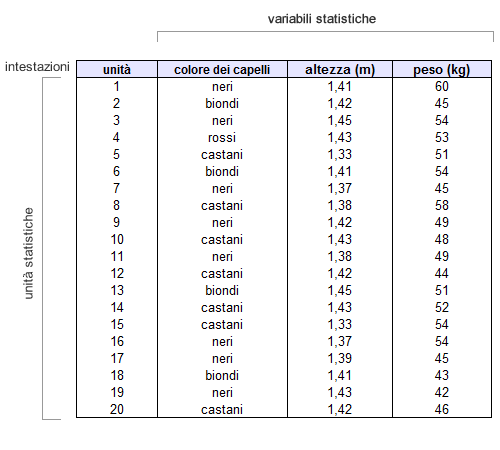
- Esempio di dati grezzi. Nella seguente matrice sono rappresentati i dati grezzi della rilevazione statistica prima i essere raggruppati in frequenze statistiche. Come si può notare, i dati grezzi sono molto più difficili da interpretare rispetto ai dati sintetici delle frequenze statistiche.