Statistica inferenziale
La statistica inferenziale è la branca della statistica che studia le rilevazioni parziale e campionarie su una popolazione. È anche detta inferenza statistica. Si occupa di analizzare i dati ottenuti da un campione della popolazione per stimare un fenomeno statistico sull'intera popolazione di riferimento.
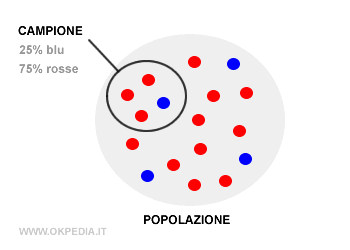
Definizione di inferenza statistica
L'inferenza statistica stima le caratteristiche complessive di una popolazione a partire da un campione limitato.
L'estensione dei risultati da una campione alla popolazione è detta inferenza.
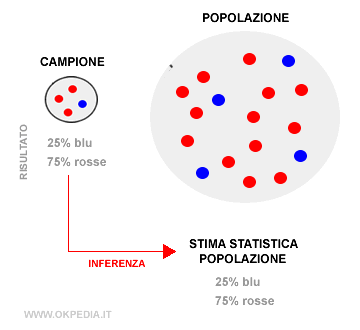
La stima è un'approssimazione statistica del risultato di un'indagine sull'intera popolazione.
Nota. La stima ha costi e tempi di realizzazione molto più bassi rispetto a un indagine sull'intera popolazione, perché è effettuata su un sottoinsieme più piccolo ( campione ). Tuttavia, essendo un'approssimazione la stima è soggetta a un margine di errore.
Esistono diverse tecniche di rilevazione e di analisi del campione. Uno dei principali argomenti della statistica inferenziale è la teoria delle probabilità.
A cosa serve la statistica inferenziale
La statistica inferenziale consente di osservare e interpretare un fenomeno statistico quando non è possibile o è troppo costoso effettuare un'indagine statistica sull'intera popolazione.
Esempio. Se la verifica di qualità di un prodotto comporta la distruzione dello stesso, tale controllo non può essere applicato su tutta la produzione in quanto sarebbe interamente distrutta.
Effettuando la verifica soltanto su un campione di prodotti è possibile ottenere una stima approssimativa del numero dei prodotti difettosi dell'intera produzione.
Cos'è un campione
Un campione è un sottoinsieme rappresentativo delle unità statistiche della popolazione.
Esistono diverse tecniche di campionamento.
Un esempio pratico
Una macchina produce ogni ora Y uova di cioccolata inserendovi dentro una sorpresa.
Ad esempio, cento uova di Pasqua ( Y=100 ).
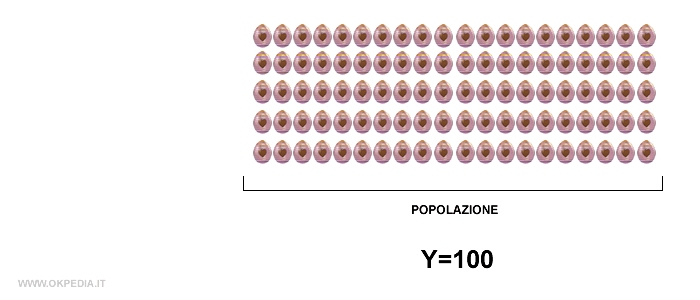
Tuttavia, a volte la macchina va in errore e non inserisce la sorpresa dentro l'uovo.
Non è però possibile controllare tutte le uova, perché la verifica comporta la distruzione del prodotto.
Esempio. Per verificare se un uovo di cioccolata contiene la sorpresa bisogna rompere l'uovo. Una volta rotto, la merce non può essere più venduta.
Quindi, per stimare la percentuale degli errori e dei difetti di fabbricazione dell'intera produzione ( Y ) viene effettuato un controllo su un campione rappresentativo di X prodotti ( X<Y ).
Ad esempio, un campione di dieci uova ( X=10 )
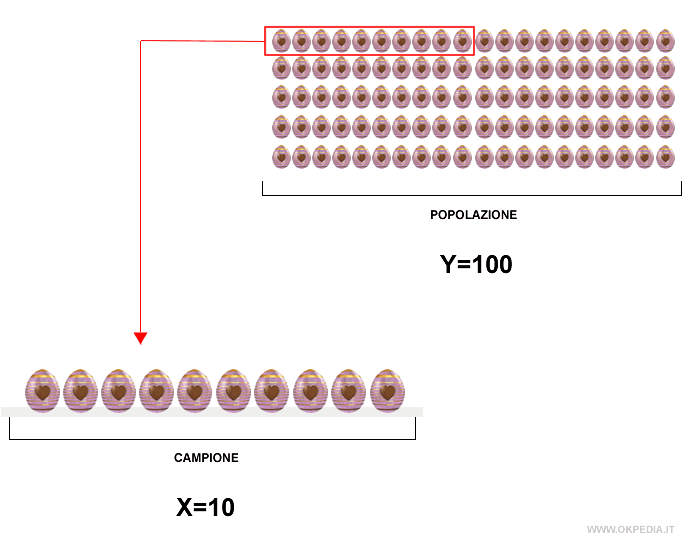
Come scegliere il campione. La scelta delle unità statistiche del campione può essere effettuata in modo casuale ( aleatorio ) o seguendo un criterio oggettivo tale da garantire la rappresentatività del campione nei confronti dell'intera popolazione
Nei dieci prodotti del campione soltanto un uovo non contiene la sorpresa.
Quindi la precentuale di merce difettosa è pari al 10% ossia 1 su 10.
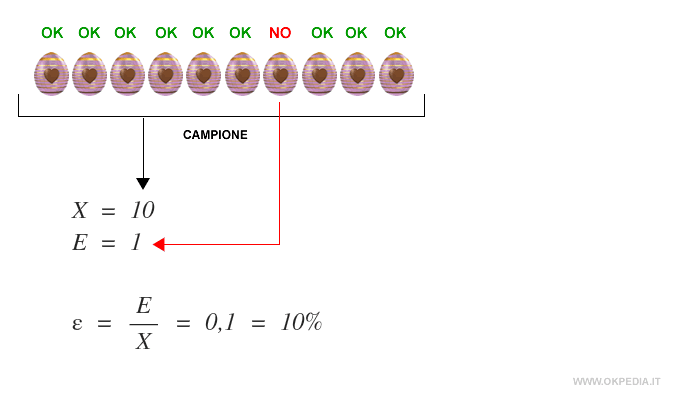
Il risultato dell'indagine campionaria viene esteso al resto della popolazione.
Pertanto si stima che l'intera produzione Y sia composta per il 10% da uova senza sorpresa ossia 10 su 100.
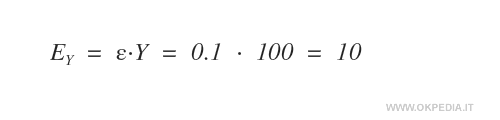
Essendo un'analisi condotta soltanto su una parte della popolazione ( campione ), i risultati di un'indagine statistica inferenziale hanno un margine di errore.
Esempio: gli exit poll. Un'applicazione pratica della statistica inferenziale sono gli exit poll durante le elezioni. Gli exit poll sono un'indagine statistica condotta su un campione di elettori, ai quali si chiede di dichiarare in segreto il proprio voto all'uscita dai seggi elettorali. I dati raccolti dagli exit poll sono elaborati per fornire una stima sintetica del risultato elettorale in attesa che siano ultimate le operazioni di spoglio dei voti. Se il campione prescelto di elettori è rappresentativo dell'intera popolazione degli elettori, allora la distribuzione dei voti negli exit poll è tendenzialmente simile a quella reale ( scrutinio elettorale ).
