Circoscrizione ( logica )
Nella logica la circoscrizione è una forma di logica non monotona in cui sono specificate le eccezioni alla regola generale. Questa forma di logica consente di circoscrivere i casi eccezionali, ossia gli enunciati che appartengono a un determinato insieme ( categoria ) senza rispettare tutte le proprietà e regole generali dell'insieme stesso. Ad esempio, nell'insieme degli uccelli è possibile affermare che "gli uccelli volano" ed è valida la conseguenza logica "se è un uccello allora può volare". Nel formalismo della logica del primo ordine, la conseguenza logica può essere scritta nel seguente modo:
Uccelli(x) ⇒ Vola(x)
Se x appartiene all'insieme degli uccelli, allora x può volare. La regola può essere applicata nella maggior parte dei casi ( es. gabbiani, rondini, ecc. ) ma esistono anche degli uccelli che non sanno volare ( es. pinguini ). Nella logica classica la presenza dei pinguini nell'insieme degli uccelli causerebbe una grave contraddizione, in quanto non varrebbe la conseguenza logica che collega l'enunciato di premessa "è un uccello" con l'enunciato di conclusione "gli uccelli volano". La circoscrizione consente di superare questo problema introducendo un ulteriore predicato di non verità ( anormalità ).
Uccelli(x) ∧ ¬ Anormaleuccelli(x) ⇒ Vola(x)
Se x appartiene all'insieme degli uccelli ( true ) e non appartiene all'insieme dei casi anomali ( false ), allora x può volare ( true ). Si può facilmente notare che la clausola dei casi anomali è negata ( ¬ ) . Se x non è anomalo, la negazione della clausola è vera ( true ) e anche la conseguenza logica ( uccelli⇒vola ) è vera. Viceversa, se x è anomalo la clausola negata è falsa ( false ) e la conseguenza logica ( uccelli⇒vola ) non è applicata. Ad esempio:
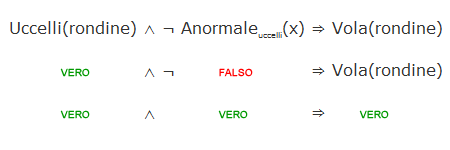
Nel caso delle rondini entrambe le clausole di premessa sono vere, le rondini sono uccelli e non sono casi anomali, è quindi valida la conseguenza "le rondini volano".

Viceversa, nel caso dei pinguini è vera soltanto la prima premessa ( "i pinguini sono uccelli" ) in quanto i pinguini sono inclusi nell'insieme delle eccezioni ( true ) e non è, quindi, applicabile la conseguenza logica "i pinguini volano". In questo modo la circoscrizione logica consente di evitare il problema delle eccezioni alla regola.
 Comprensione della realtà. La realtà è complessa e le eccezioni alla regola sono frequenti. Queste caratteristiche rendono difficilmente rappresentabile la realtà con la logica classica. La circoscrizione logica, invece, consente all'agente logico di analizzare gli aspetti logici della realtà, evitando le molteplici contraddizioni logiche che possono venirsi a creare a causa della presenza dei casi eccezionali nella rappresentazione della conoscenza.
Comprensione della realtà. La realtà è complessa e le eccezioni alla regola sono frequenti. Queste caratteristiche rendono difficilmente rappresentabile la realtà con la logica classica. La circoscrizione logica, invece, consente all'agente logico di analizzare gli aspetti logici della realtà, evitando le molteplici contraddizioni logiche che possono venirsi a creare a causa della presenza dei casi eccezionali nella rappresentazione della conoscenza. Numero delle eccezioni. Nella circoscrizione logiche i casi eccezionali devono essere esplicitamente dichiarati nell'elenco dei casi anomali. Questa forma di logica è utile quando il numero delle eccezioni alla regola è abbastanza limitato. Viceversa, quando il numero dei casi eccezionali è molto alto, si potrebbero creare delle difficoltà insormontabili sia in termini di complessità della rappresentazione che in termini di complessità spaziale e temporale per elaborare i casi anomali/eccezionali.
Numero delle eccezioni. Nella circoscrizione logiche i casi eccezionali devono essere esplicitamente dichiarati nell'elenco dei casi anomali. Questa forma di logica è utile quando il numero delle eccezioni alla regola è abbastanza limitato. Viceversa, quando il numero dei casi eccezionali è molto alto, si potrebbero creare delle difficoltà insormontabili sia in termini di complessità della rappresentazione che in termini di complessità spaziale e temporale per elaborare i casi anomali/eccezionali.- Ordine di priorità delle eccezioni. L'uso delle eccezioni potrebbe generare altre situazioni ambigue. Ad esempio, date due conseguenze logiche A(x)⇒C(x) e B(x)⇒¬C(x) in cui l'elemento x appartiene ad A e B ed è un'eccezione per entrambi, si ottiene un risultato ambiguo ( eccezioni in conflitto ) poiché per l'elemento x non varrebbe né C(x), né l'opposto ¬C(x). Si può uscire da queste ulteriori situazioni conflittuali fissando un ordine di priorità o di preferenza tra le eccezioni. Ad esempio, affermando che le eccezioni di B sono più importanti rispetto alle eccezioni di A, nel caso precedente è possibile affermare che la conseguenza A(x)⇒C(x) è valida, nonostante l'elemento x sia una eccezione di A(x)⇒C(x), quando l'elemento x è un'eccezione di B(x)⇒¬C(x).
