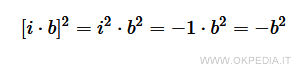Unità immaginaria dei numeri complessi
L'unità immaginaria (i) dei numeri complessi è il numero $$ i = (0;1) $$ il cui quadrato è il numero reale -1 $$ i^2=-1 $$ ovvero $$ i = \sqrt{-1} $$ È il numero non reale più semplice.
L'unità immaginaria è alla base dei numeri complessi.
In forma algebrica qualsiasi numero complesso z è composto dalla somma di un numero reale (a) e di un numero immaginario (ib)
$$ z = a + i \cdot b $$
Dove i è l'unità immaginaria mentre a e b sono due numeri reali.
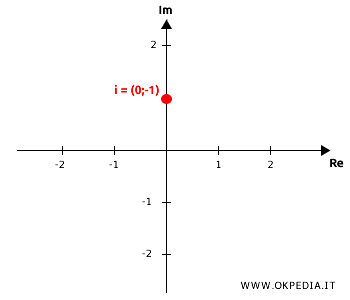
In alternativa, qualsiasi numero complesso può anche essere rappresentato come coppia di numeri reali. $$ z = (a;b) $$ In questa forma l'unità immaginaria è il punto alle coordinate cartesiane $ i =(0;1) $ del piano complesso di Gauss.
Il quadrato dell'unità immaginaria è -1
$$ i^2 = -1 $$
Per dimostrarlo basta moltiplicare l'unità immaginaria come un numero complesso \( i = 0 + 1i \) per se stessa ed espandendo il quadrato
$$ i^2 = (0 + 1i)^2 $$
$$ i^2 = 0^2 + 2 \cdot 0 \cdot 1i + (1i)^2 $$
$$ i^2 = 0 + 0 + 1 \cdot i^2 $$
Poiché \( i^2 \) è definito come \( -1 \), otteniamo:
$$ i^2 = -1 $$
Quindi, il calcolo in forma algebrica conferma che \( i^2 = -1 \).
Lo stesso risultato si ottiene moltiplicando l'unità immaginaria nella forma i=(0,1) per se stessa con la regola del prodotto tra due numeri complessi. $$ i^2 = (0;1) \cdot (0;1) $$ $$ i^2 = (0 \cdot 0 - 1 \cdot 1 ; 0 \cdot 1 + 1 \cdot 0 $$ $$ i^2 = (-1;0) $$
L'origine dell'unità immaginaria
I numeri complessi nascono per trovare una soluzione alle radici dei numeri negativi.
Non esiste alcun numero reale -a che moltiplicato n volte per stesso, dove n è un numero pari, dia come risultato -a.
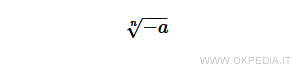
Il più semplice di questi numeri non reali è la radice quadrata (n=2) di a=-1.
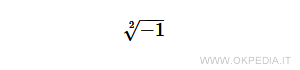
Alla radice quadrata di -1 viene assegnato convenzionalmente il nome di unità immaginaria i perché consente di ottenere tutti gli altri numeri non reali.
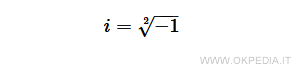
Il quadrato dell'unità immaginaria è il numero reale -1.
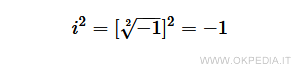
Qualsiasi numero non reale può essere espresso tramite l'unità immaginaria i.
Esempio
La radice quadrata di -4 è un numero non appartenente all'insieme dei numeri reali.
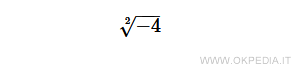
Per risolvere la radice quadrata di un numero negativo si può usare l'unità immaginaria.
Il numero -4 può essere scritto in una forma equivalente come prodotto algebrico di -1 per 4
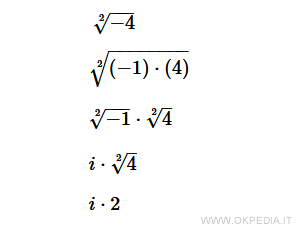
Quest'ultimo è detto numero immaginario puro.
Grazie all'unità immaginaria i è quindi possibile risolvere la radice quadrata di un numero negativo.
Numero immaginario
Il prodotto tra l'unità immaginaria i e un numero reale (b) qualsiasi è detto numero immaginario.
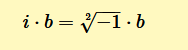
Esempio
Il quadrato di un numero immaginario ib è un numero reale -b2