Modulo del numero complesso
Il modulo di un numero complesso misura la lunghezza del vettore che collega l'origine con il numero complesso sul piano di Gauss. Si indica con due barre verticali |z| = |a±ib| 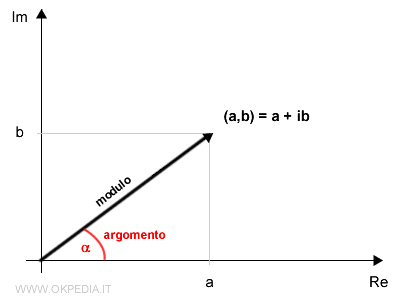
Come calcolare il modulo di un numero complesso
Dal punto di vista geometrico qualsiasi numero complesso, con parte reale diversa da zero, traccia sul piano un triangolo rettangolo.
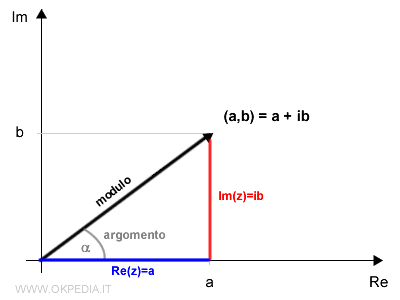
La parte reale Re(z) e la parte immaginaria Im(z) del numero complesso z misurano la lunghezza dei due cateti del triangolo.
L'ipotenusa del triangolo è, invece, il modulo del numero complesso.
Pertanto, per calcolare il modulo di un numero complesso si usa il teorema di Pitagora.
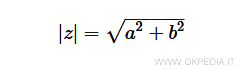
Nota. Il modulo del numero complesso |z| è uguale al modulo del numero complesso opposto |-z| e del numero complesso coniugato |z'| poiché la lunghezza dell'ipotenusa è sempre la stessa, ciò che cambia è l'argomento ossia l'angolo del vettore sul piano di Gauss.
Esempio
Il numero complesso z=3+2i individua il punto (3,2) sul piano di Gauss.
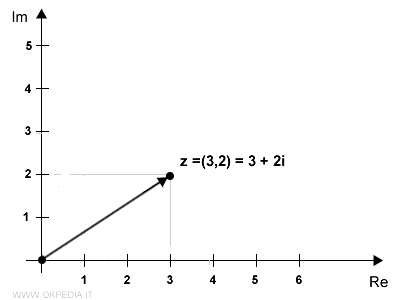
Nota. Tra i numeri complessi e i punti del piano c'è una relazione biunivoca. Pertanto, ogni punto del piano individua uno e un solo numero complesso e viceversa.
Il punto (3,2) sul piano, la sua proiezione sull'asse reale (3,0) e l'origine (0,0) formano un triangolo.
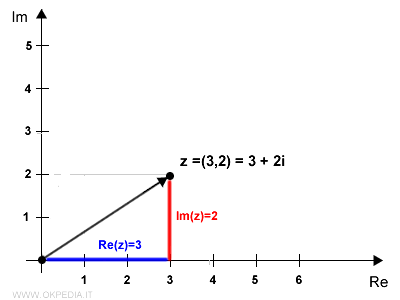
La parte reale e immaginaria del numero complesso misurano la lunghezza dei cateti.
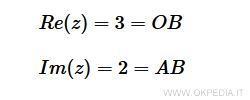
Per calcolare l'ipotenusa si applica il teorema di Pitagora.
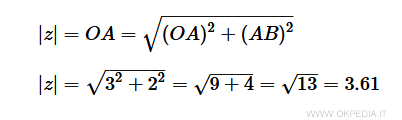
Il modulo |z| del numero complesso z=3+2i è uguale a 3.61.
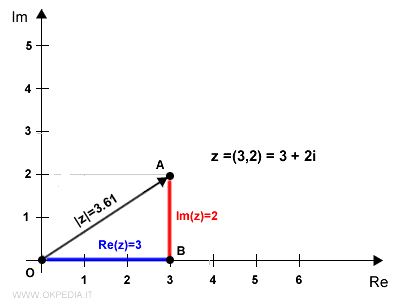
Nota. Anche il modulo del numero complesso coniugato z'=3-2i e del numero opposto -z=-3-2i è uguale 3.61 perché la lunghezza del vettore è la stessa
