Numeri complessi
I numeri complessi sono un insieme di numeri composti dalla somma algebrica di un numero reale (a) e di un numero immaginario (ib).
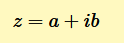
In matematica l'insieme dei numeri complessi è indicato con il simbolo C.
Gli elementi a,b di un numero complesso sono una coppia ordinata di numeri reali.
- Il primo numero reale (a) è detto parte reale del numero complesso.
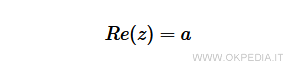
- Il secondo numero reale (b) è detto parte immaginaria del numero complesso.
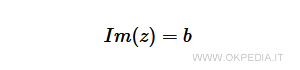
- L'elemento i è detto unità immaginaria ed è posto per definizione pari alla radice quadrata di -1. L'unità immaginaria è indicata con la lettera i oppure con la lettera j.
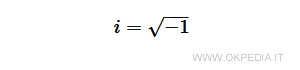
Nota. I numeri complessi possono essere rappresentati in varie forme. La forma z=a+ib è detta forma cartesiana.
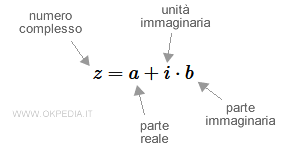
Il primo termine a è un numero reale mentre il termine ib è un numero immaginario. Dove per numero immaginario si intende un qualsiasi multiplo dell'unità immaginaria (i).
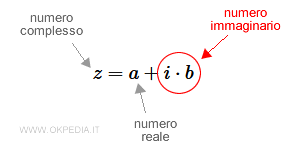
La rappresentazione dei numeri complessi sul piano di Gauss
Un numero complesso si può rappresentare anche come coppia ordinata di numeri reali.
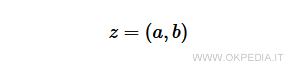
Questo permette di rappresentare ogni numero complesso su un piano cartesiano, detto piano di Gauss, assegnando la parte reale all'ascisse e la parte immaginaria alle ordinate.
Il numero complesso è un vettore che congiunge l'origine del piano con il punto (a,b).
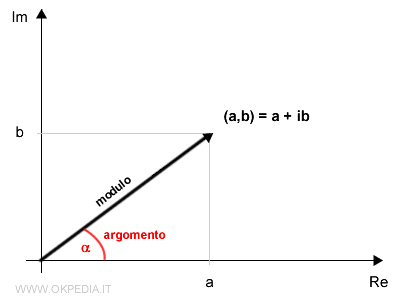
Tra i punti del piano e i numeri complessi c'è una corrispondenza biunivoca.
Ogni punto del piano è un numero complesso e viceversa.
Pertanto, ogni numero complesso sul piano può essere anche indicato fornendo la lunghezza del vettore (modulo) e l'angolo α rispetto all'asse delle ascisse (argomento o abbreviato arg).
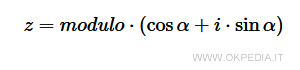
Quest'altra rappresentazione è detta forma trigonometrica.
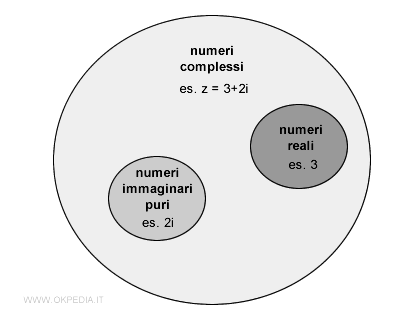
Nota. L'insieme dei numeri complessi C è un insieme più grande dei numeri reali R. L'insieme dei numeri complessi è composto dai numeri complessi, dai numeri reali e dai numeri immaginari puri. Ogni numero reale può essere scritto nella forma z=a+i·0. Quindi, l'asse Re del piano di Gauss coincide con l'insieme dei numeri reali. Ogni numero immaginario puro può essere scritto nella forma z=0±i·b. Quindi, l'asse Im del piano di Gauss coincide con l'insieme dei numeri immaginari puri. Gli altri punti del piano sono numeri complessi veri e propri.
Esempio
Prendiamo due numeri complessi in forma cartesiana
z' = 3 + 2i
z'' = 1 + 4i
La rappresentazione dei numeri sul piano di Gauss è la seguente
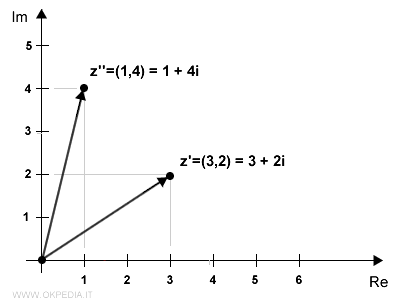
La stessa rappresentazione si può ottenere usando la forma trigonometrica dei numeri.
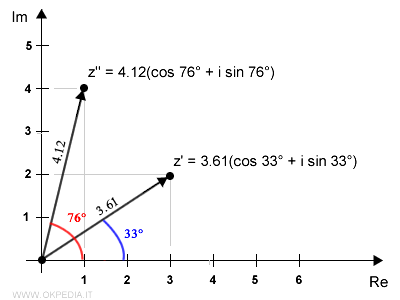
Il numero z' ha modulo pari a 3.61 e un argomento pari a 33°.
Il numero z'' ha un modulo pari a 4.12 e un argomento pari a 76°.
