Media aritmetica in una tabella di frequenze
La media aritmetica delle frequenze di una tabella statistica è determinata dal rapporto tra la somma algebrica dei prodotti di ciascuna frequenza per la propria modalità, e la somma delle frequenze.
Un esempio pratico
Nella seguente tabella sono rappresentati gli studenti di una classe per età. Le frequenze assolute sono il numero degli studenti per ogni età.
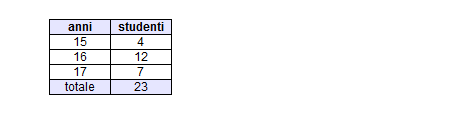
Pur non conoscendo l'età di ciascuno studente, possiamo calcolare l'età media della classe. Moltiplichiamo ogni frequenza assoluta per la sua modalità ( età = e sommiamo tutti i prodotti ( S1 ). Nell'esempio la somma dei prodotti è uguale a 371.
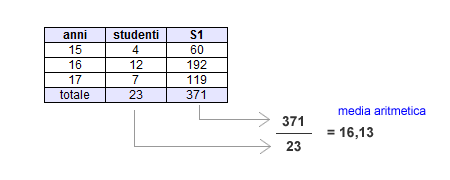
Dividendo la somma dei prodotti ( 371 ) per la somma delle frequenze assolute ( 23 ) otteniamo la media aritmetica della tabella ( 16,13 ). L'età media degli studenti è di 16,13 anni.
La media aritmetica delle classi di frequenze
La media aritmetica può essere calcolata anche se la distribuzione è suddivisa in classi di frequenze.
Ad esempio, nella seguente tabella sono presenti tre classi di frequenze. Ogni classe di frequenza è associata a una particolare fascia d'età ( 20-30, 30-40 e 40-50 ) dei lavoratori di un'azienda.

Per calcolare la media aritmetica della popolazione, dobbiamo individuare il valore centrale di ciascuna classe di frequenza.
Ad esempio, nella prima classe di frequenza sono inclusi tutti i lavoratori con età compresa tra 20 e 30 anni. Il valore centrale di questa classe è 25 ossia (20+30)/2.
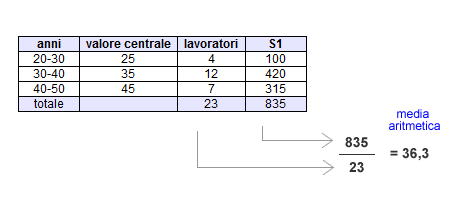
Moltiplichiamo ciascuna frequenza assoluta per il valore centrale della sua classe di frequenza. Il valore medio di ciascuna classe è considerato come il peso della classe.
La somma di tutti i prodotti delle frequenze per i valori centrali è pari a 835 ( S1 ). La somma di tutte le frequenze assolute è pari a 23.
Il rapporto tra la somma dei prodotti delle frequenze (835) e la somma di tutte le frequenze assolute (23), ci permette di calcolare la media aritmetica dell'intera popolazione. L'età media dei lavoratori è pari a 36,3.
