Media aritmetica ponderata
La media aritmetica ponderata è calcolata sommando tutti i valori delle modalità per un coefficiente che definisce il suo peso ( importanza ) rispetto agli altri valori della distribuzione.
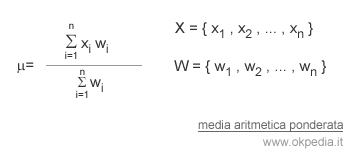
Data una variabile statistica X con n modalità quantitative { X1, X2, ... , Xn }, è possibile associare a ciascuna di esse un peso wi ( coefficiente di importanza ) in base alla sua frequenza di ripetizione.
Un esempio di media pesata ( o ponderata )
Nella seguente tabella sono rappresentati i voti di esame di una classe composta da venti studenti.
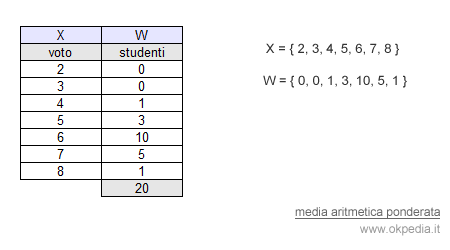
La variabile statistica X è il voto d'esame e le modalità Xn sono tutti i possibili voti da 2 a 8. A ogni modalità è associata la frequenza degli studenti che hanno preso quel voto. Ad esempio, cinque studenti hanno preso il voto sette al compito in classe.
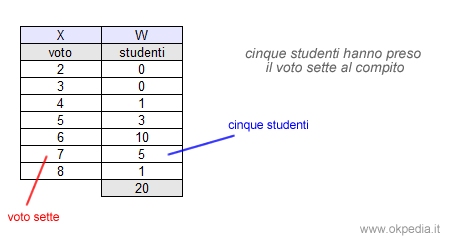
La precedente tabella è una distribuzione di frequenze e le frequenze possono essere considerate come i pesi delle rispettive modalità. Per ogni modalità (X) è possibile calcolare il prodotto (XW) con la rispettiva frequenza (W).
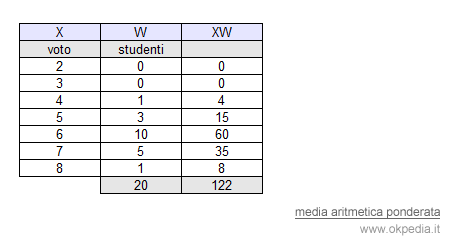
Per calcolare la media ponderata è sufficiente dividere la somma dei prodotti dei valori pesati ( Σ xi wi ) per la somma dei pesi ( Σ wi ).
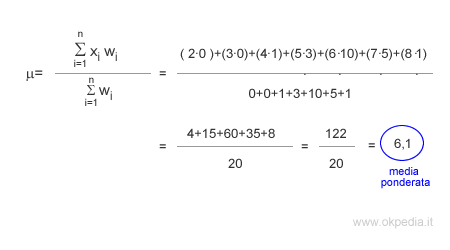
La media ponderata dei voti è 6,1. Abbiamo calcolato la media ponderata della distribuzione di frequenze X.
La differenza tra la media ponderata e la media aritmetica
La media aritmetica è un caso particolare di media ponderata, quello in cui tutte le modalità hanno un peso uguale pari a uno ( Wi=1 ).
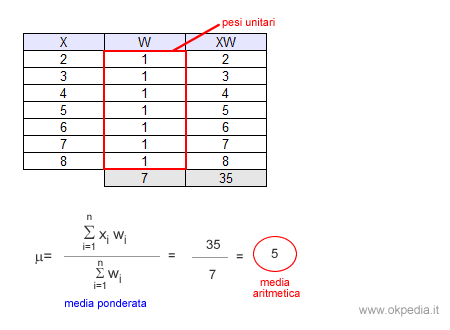
Applicando i pesi unitari (W=1) la media ponderata si trasforma in una semplice media aritmetica delle modalità X. Nel nostro esempio, la media aritmetica dei valori è uguale a 5.
La media ponderata con pesi arbitrari
L'attribuzione dei pesi alle modalità può anche essere stabilita arbitrariamente. Questa scelta può essere giustificata per motivi strategici.
Ad esempio, si potrebbe associare ai voti più bassi un peso maggiore, allo scopo di spingere lo studente a studiare con continuità.
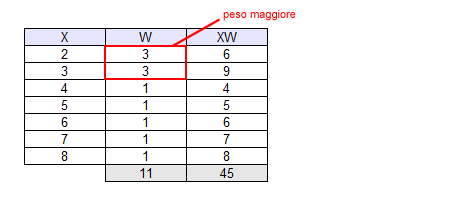
Se i voti bassi avessero un peso maggiore rispetto a quelli più alti, lo studente non riuscirebbe a recuperare facilmente un'insufficienza grave ( voto 2 o 3 ) e sarebbe incentivato a seguire le lezioni con attenzione e studiare di più.
Ad esempio, nei primi due trimestri dell'anno lo studente prende due voti alti (8), mentre nel terzo trimestre smette di studiare e prende un voto basso (2).
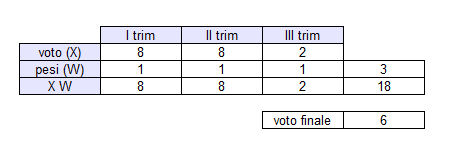
Con la media aritmetica il suo voto finale è 6 e lo studente viene promosso.
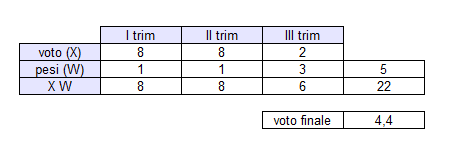
Con la media ponderata con pesi arbitrari, invece, il voto basso ha un peso maggiore. Il voto finale è 4,4 e lo studente viene bocciato.
