Teoria della rendita del consumatore di Marshall
Nella teoria della rendita del consumatore ( o teoria del sovrappiù) Alfred Marshall trova un collegamento diretto tra la teoria dell'utilità marginale e la teoria della domanda. Usa la differenza tra i prezzi marginali e i prezzi di mercato per misurare l'utilità del consumatore.
Marshall confronta il prezzo di mercato della merce (p*) con il prezzo marginale p(q) che il consumatore è disposto a pagare ( p1, p2, ecc. ) per ogni unità aggiuntiva di consumo ( q1, q2, ecc. ).
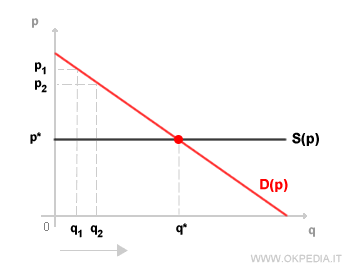
La somma delle differenze p(q)-p*, per ogni unità di consumo q, fornisce la misurazione dell'utilità ottenuta dal consumatore, ossia il guadagno di utilità ottenuto dal consumatore con il consumo della quantità q del bene.
Le prime unità di consumo forniscono un'utilità marginale più alta.
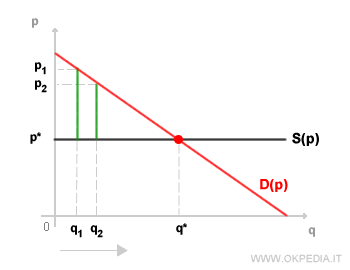
Esempio. La differenza (p1-p*) è maggiore di (p2-p*) perché la prima unità di consumo del bene fornisce un'utilità marginale più alta rispetto alla seconda. E così via.
L'utilità marginale si riduce con il consumo delle unità aggiuntive fino ad annullarsi del tutto in corrispondenza del prezzo di mercato ( ultima unità aggiuntiva di consumo ).
In corrispondenza del prezzo p* si verifica l'equilibrio di mercato (E), il punto in cui la domanda eguaglia l'offerta D(p)=S(p).
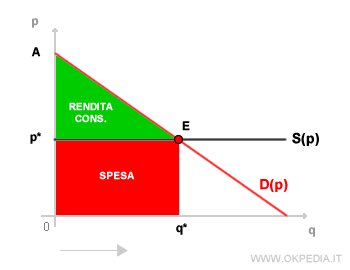
Complessivamente il consumatore ottiene un guadagno lordo di utilità pari all'area sottostante la curva di domanda (OAEq*). Nel grafico è la somma dell'area verde e rossa.
D'altra parte, per consumare la quantità q del bene paga un costo pari all'area sottostante il prezzo di mercato (Op*Eq*). Nel grafico è l'area di colore rosso.
La differenza tra le due aree determina la rendita del consumatore ( o sovrappiù del consumatore ), ossia il guadagno complessivo di utilità ottenuto dal consumatore.
Nota. Nel grafico precedente la rendita del consumatore è l'area verde p*AE a forma di triangolo. In questo modo geometrico Alfred Marshall misura l'utilità del consumatore con la teoria della domanda e del prezzo di mercato.
