Teoria dei quanti
La teoria dei quanti si basa sul concetto di quantizzazione dell'energia di una radiazione elettromagnetica. Viene formulata nel 1900 dal fisico tedesco Max Planck.
Secondo Planck, l'energia può assumere soltanto valori multipli interi e mai frazionari di un valore fondamentale detto quanto.
Le onde elettromagnetiche sono emesse sotto forma di pacchetti unitari, detti quanti. Non è quindi possibile emettere le onde a un ritmo arbitrario.
Cos'è il quanto?
Il quanto è una quantità minima e indivisibile dell'energia che può essere assunta in quantità discrete ( non continue ) da una grandezza fisica. È una particella fondamentale associata all'interazione.
L'energia elettromagnetica è la prima grandezza a essere quantizzata con il quanto di energia, successivamente detto fotone. Il quanto di energia E è pari alla costante di Planck ( h ) per la frequenza della radiazione ( v ).
E = h v
Ogni quanto veicola una quantità di energia tanto maggiore (E), quanto più alta è la frequenza (v) delle onde.
In questo modo Planck considera tutte le radiazioni elettromagnetiche, ivi compresa la luce, come una grandezza discreta e non come una grandezza continua.
Perché Planck elabora la teoria dei quanti?
Max Planck elabora il concetto del quanto per spiegare il fenomeno delle radiazioni emesse da un corpo nero.
Secondo le leggi scientifiche dell'epoca, un corpo molto caldo dovrebbe emettere onde elettromagnetiche con la stessa quantità di energia (E) su tutte le frequenze (v).
Questa convinzione genera però un paradosso. Essendo illimitate le frequenze (v), il corpo dovrebbe irraggiare una quantità infinita di energia.
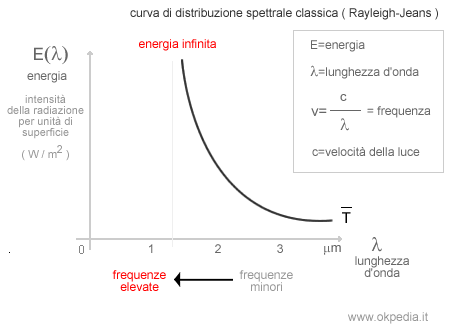
Nel precedente grafico viene mostrata la distribuzione dell'intensità energetica delle onde elettromagnetiche al variare della lunghezza d'onda ( λ ) per una data temperatura T.
Quanto più aumenta la frequenza delle onde ( larghezza d'onda inferiore ) tanto più aumenta l'intensità energetica ( E ) della radiazione per unità di superficie irraggiata. Questa distribuzione classica è conosciuta come distribuzione Rayleigh-Jeans.
Come anticipato, questa teoria crea diversi paradossi. Ad esempio, secondo i fisici inglesi Rayleigh e James Jeans una stella dovrebbe disporre di una quantità infinita di energia. Il che è ovviamente impossibile.
Qual è la soluzione di Planck?
Nella teoria di Planck le onde elettromagnetiche sono emesse sotto forma di pacchetti unitari ( quanti ) e non è possibile emettere le onde a un ritmo arbitrario. Inoltre, l'energia di ogni quanto è correlata alla frequenza delle onde.
Pertanto, le onde ad alta frequenza emesse da un corpo caldo richiedono una quantità maggiore di energia (E). Se il consumo è superiore all'energia disponibile, le radiazioni ad alta frequenza si riducono e il corpo perde energia.
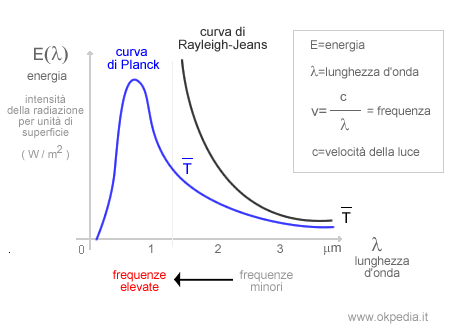
Nel precedente grafico è rappresentata la curva di Planck per una temperatura T. L'intensità della radiazione per unità di superficie raggiunge il suo massimo a una determinata frequenza, poi si riduce.
La curva di Planck riesce a rappresentare meglio la distribuzione spettrale di un corpo nero, rilevata nel corso degli esperimenti.
Si risolve così il paradosso della curva di Rayleigh-Jeans. Nelle frequenze più elevate della radiazione non si registra la crescita infinita dell'intensità energetica, poiché quest'ultima decresce.
Dalla teoria dei quanti alla meccanica quantistica
Planck introduce il quanto di energia come un artificio di calcolo, al solo scopo per spiegare la curva delle emissioni di un corpo caldo.
La comunità scientifica non si accorge immediatamente della portata rivoluzionaria di questa teoria per l'intera scienza.
La teoria dei quanti costituisce la base concettuale su cui viene costruita la meccanica quantistica che descrive i fenomeni fisici, come le radiazioni e la materia, sia come fenomeni ondulatori che particellari.
Qual è la differenza con la meccanica classica?
Nella meccanica classica le grandezze sono continue. Nella meccanica quantistica, invece, le grandezze assumono valori discreti e variano secondo i valori multipli di un valore fondamentale indivisibile ( quanto ).
