Equazioni differenziali
In matematica le equazioni differenziali sono uno strumento del calcolo differenziale.
La definizione di equazione differenziale
Data una funzione reale incognita u(x) definita nel dominio D⊆R e un numero reale x appartenente allo stesso dominio, l'equazione differenziale individua la relazione F tra il numero x, la funzione incognita u(x) e le sue derivate u(n)(x) entro un determinato ordine n di derivazione.
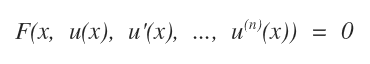
L'equazione può essere rappresentata anche nella seguente forma alternativa:
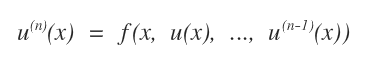
L'ordine massimo della derivata che compare nell'equazione è detto ordine dell'equazione differenziale.
La spiegazione delle equazioni differenziali
Le equazioni differenziali risolvono i problemi in cui la soluzione non è un numero reale ma una funzione incognita u(x).
La storia delle equazioni differenziali. La teoria delle equazioni differenziali nasce nel XIX secolo per opera dei matematici Cauchy, Lipschitz, Peano. Tuttavia, i primi studi sulle equazioni differenziali sono antecedenti e risalgono al XVII secolo.
Spesso non è possibile ricostruire la funzione incognita u(x) che spiega un fenomeno, ma soltanto ottenere informazioni sulle funzioni derivate u(n)(x) entro un certo ordine.
Il caso più semplice
Nel caso più semplice delle equazioni differenziali del primo ordine, per individuare la funzione incognita u(x) a partire dalle funzioni derivate u(n)(x) si utilizzano gli integrali.
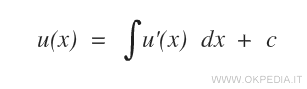
Si può facilmente notare che l'integrale non individua una soluzione ma infinite soluzioni che differeiscono tra loro per la costante c.
Per questa ragione, in genere un'equazione differenziale ammette un numero infinito di soluzioni.
Tuttavia, come già anticipato, in altri casi i dati del problema non rendono possibile calcolare la funzione incognita generale u(x) ma soltanto le sue derivate u(n)(x).
Le equazioni differenziali del primo ordine
Le equazioni differenziali del primo ordine sono quelle in cui compare soltanto la derivata prima della funzione incognita.
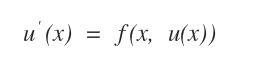
Primo caso ( semplice )
Nel caso più semplice delle equazioni del primo ordine la derivata u'(x) è in funzione soltanto della variabile indipendente x.
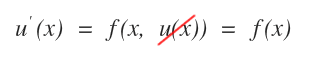
In quest'ultimo caso, la soluzione dell'equazione differenziale si riduce al calcolo dell'integrale per individuare la primitiva di u'(x) ossia la u(x).
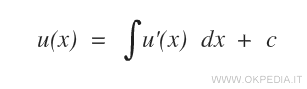
Esempio
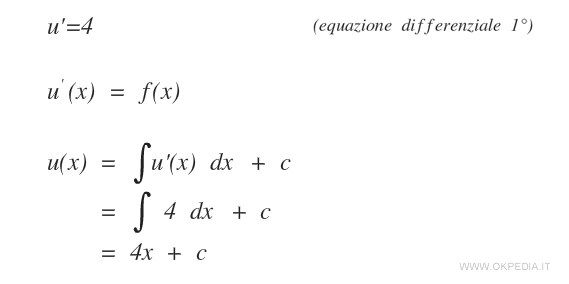
Secondo caso
Quando invece la funzione derivata u'(x) dipende anche dalla stessa funzione u(x)
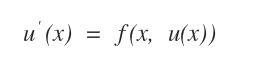
per trovare la soluzione non è più sufficiente il calcolo dell'integrale e si utilizza la formula generale dell'equazione differenziale di primo grado, dove a(x) e f(x) sono due funzioni continue.
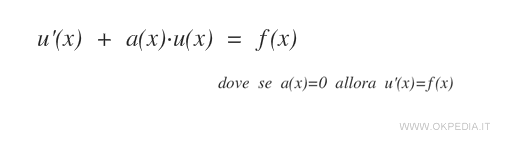
Quando a(x) non è nulla si moltiplica l'equazione per il fattore integrante eA(x) dove A(x) è una primitiva di a(x).
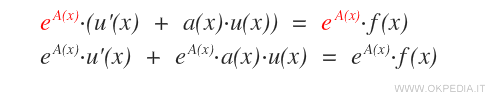
Così facendo, il primo membro dell'equazione può essere interpretato come la derivata di eA(x)u(x).
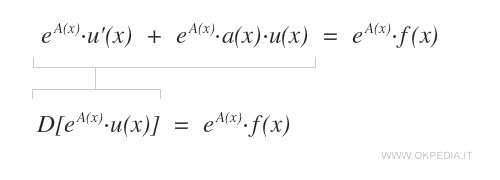
A questo punto si calcola l'integrale indefinito di entrambi i membri
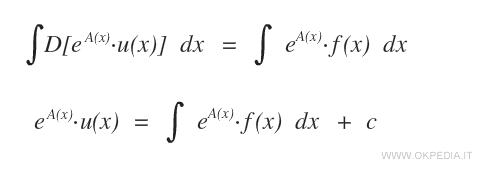
Per eliminare eA(x) nel membro di sinistra, si moltiplicano entrambi i membri dell'equazione per e-A(x).
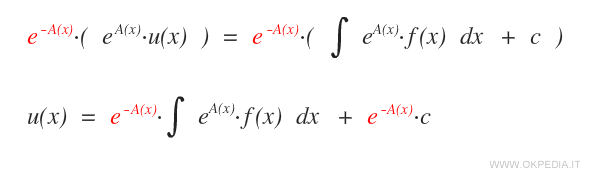
In questo modo si isola u(x) nel membro di sinistra e si ottiene la formula della soluzione generale di un'equazione differenziale lineare.
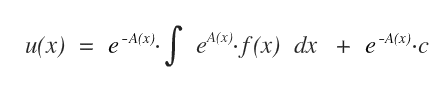
Questa formula consente di risolvere qualsiasi equazione differenziale di primo grado.
Esempio

In alcuni casi si aggiunge anche la condizione iniziale e la costante arbitraria c è assegnata al valore iniziale della y(x0).
La soluzione dell'equazione differenziale
Un'equazione differenziale può essere anche rappresentata nella seguente forma alternativa in base all'ordine.
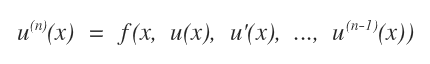
La funzione reale u che soddisfa l'equazione differenziale è detta soluzione o integrale.
La soluzione può essere generale o particolare.
- La soluzione generale individua tutti i parametri dell'equazione differenziale. Al variare dei parametri descrive tutte le soluzioni dell'equazione.
- La soluzione particolare si ottiene sostituendo i parametri dell'equazione differenziale con dei valori.
