Equazioni differenziali del primo ordine

Le equazioni differenziali del primo ordine sono equazioni differenziali in cui la derivata prima è la derivata massima della funzione incognita.

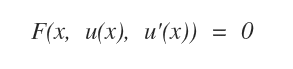
In una rappresentazione alternativa l'equazione differenziale di 1° ordine è indicata nel seguente modo:

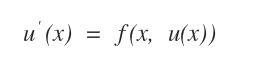
Ci sono diversi metodi di risoluzione, a seconda delle caratteristiche dell'equazione differenziale.

Equazioni differenziali semplici

Sono le equazioni differenziali di primo grado in cui nel secondo membro non compare la funzione incognita u(x).

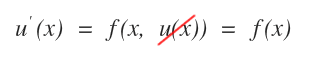
Sono considerate semplici perché sono risolubili direttamente con una integrazione.

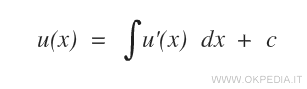
La soluzione è la funzione primitiva della funzione f(x).

Un esempio pratico

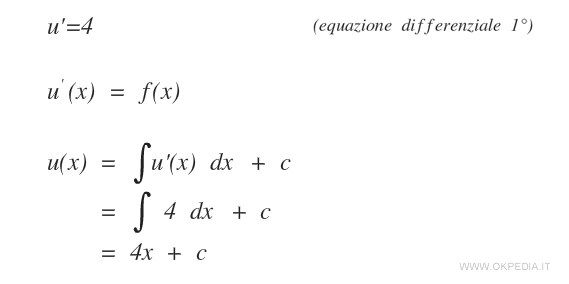
Equazioni differenziali a variabili separabili

Sono equazioni differenziali di 1° ordine che si possono ridurre alla seguente forma

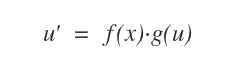
Nota. La u'(x) è la derivata della funzione incognita u(x) che vogliamo cercare. Mentre al secondo membro g(u) è una funzione dipendente dalla funzione incognita u(x), moltiplicata per una funzione f(x) dipendente da x.

Per risolvere queste equazioni si può usare la seguente procedura di calcolo:

Un esempio pratico

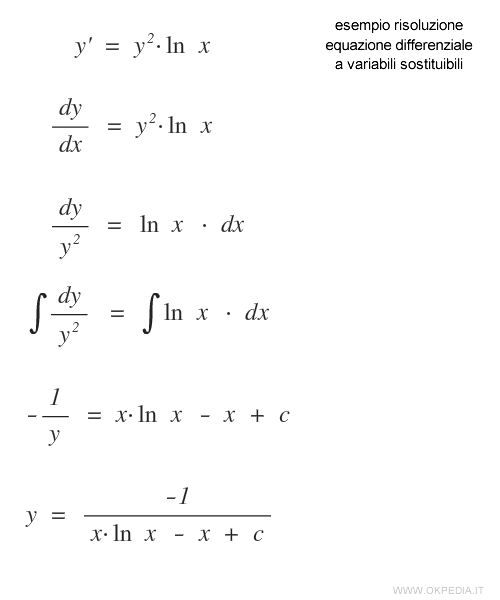
Nota. L'integrale ∫ ln x · x è stato risolto tramite il metodo dell'integrazione per parti.

Equazioni differenziali lineari

Le equazioni differenziali lineari del primo ordine sono equazioni differenziali che si presentano nella seguente forma:

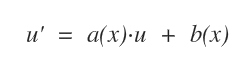
Queste equazioni si risolvono in modo diverso a seconda dei casi.

1. Se a(x)=0 l'equazione diventa u'=b(x). Quindi può essere risolta direttamente con l'integrazione come un'equazione differenziale semplice.
   
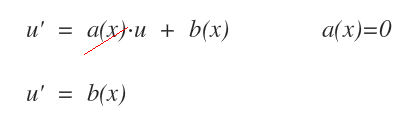
2. Se b(x)=0 l'equazione diventa u'=a(x)·u. Si dice equazione omogenea. In questo caso può essere risolta come un'equazione differenziale a variabili separabili.
   
   

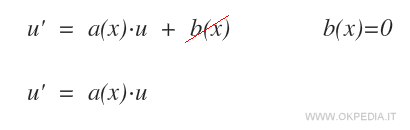
   Equazioni differenziali omogenee. Per risolvere le equazioni differenziali omogenee, oltre al metodo di risoluzione a variabili separabili, si può anche utilizzare anche il metodo del fattore integrante. La formula del metodo del fattore integrante è la seguente:
   
   Nota. Alla soluzione trovata dal metodo bisogna aggiungere sempre anche il caso u=0. La dimostrazione è la seguente: se u=0, la derivata di una costante è nulla u'=0. Quindi u'=a(x)u diventa 0=0 ed è verificata.

3. Se a(x)≠0 e b(x)≠0 l'equazione è detta equazione non omogenea. Si risolve con il metodo di Lagrange o metodo di variazione della costante.
   
   
   Si tratta di una formula generale applicabile per tutte le equazioni lineari di 1° grado, sia omogenee che non omogenee. Ad esempio, se b(x)=0 la formula diventerebbe quella usata per il calcolo della soluzione delle equazioni omogenee ossia u(x)=e^A(x)·c.
   

   Dimostrazione ed esempio pratico. La precedente formula di risoluzione delle equazioni differenziali lineari non omogenee del 1° ordine si dimostra nel seguente modo. Al termine della dimostrazione è presente un esempio pratico di applicazione della formula per il calcolo della soluzione.
   
   Nota. Come per le equazioni omogenee anche in questo caso occorre aggiungere alle soluzioni il caso u=0, perché la derivata di una costante è nulla (u'=0). Quindi l'equazione u'=a(x)u diventa 0=0 ed è verificata.