Consistenza euristica

La consistenza euristica ( monotonicità ) è una condizione di ottimalità degli algoritmi di ricerca informata. La consistenza è considerata una condizione forte di ottimalità ed è applicata alla ricerca di soluzioni nei grafi mediante la ricerca A star. Una euristica è consistente se, per ogni nodo n del grafo e ogni suo successore n', il costo stimato h(n) per raggiungere l'obiettivo è uguale o inferiore al costo di passo per arrivare da n a n' sommato al costo stimato h(n') per arrivare all'obiettivo da n'. Questa condizione può essere agevolmente spiegata con una rappresentazione grafica.

Quando l'euristica h() è consistente la funzione dei costi del cammino non è decrescente. Man mano che si prosegue nel corso del cammino il costo del cammino è crescente o, al massimo, uguale. Un'euristica consistente ( euristica monotona ) è anche una euristica ammissibile. Ciò equivale a dire che una euristica monotona garantisce che venga trovata per prima la soluzione meno costosa (soluzione ottimale). Per questa ragione la consistenza (monotonicità) è una delle condizioni di ottimalità degli algoritmi di ricerca informata ricerca A star. Una euristica consistente è sempre anche una euristica ammissibile.

Euristica ammissibile non monotona. Esistono anche euristiche ammissibili non monotone, si tratta, tuttavia, di casi molto rari.

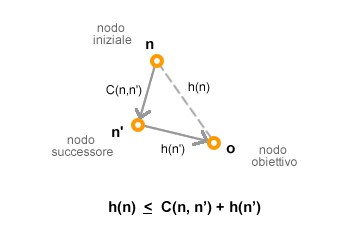
Diseguaglianza triangolare. Dal punto di vista geometrico la consistenza (monotonicità) tra tre nodi ( n, n', o ) può essere analizzata osservando la forma del triangolo formato dall'unione dei nodi. In un triangolo ogni singolo lato non può essere superiore alla somma degli altri due ( diseguaglianza triangolare ).