La rappresentazione dei dati statistici
La rappresentazione dei dati in statistica è realizzata tramite tabelle e/o grafici. I dati grezzi di una rilevazione statistica non sono facilmente interpretabili. Per rendere comprensibile l'informazione o il significato della rilevazione, è necessario operare la sintesi e la rappresentazione dei dati statistici.
La rappresentazione a tabelle
Nella rappresentazione a tabelle i dati sono organizzati all'interno delle righe e delle colonne di una matrice quadrata o rettangolare. Generalmente, in una tabella le righe identificano le modalità e le colonne le variabili statistiche.
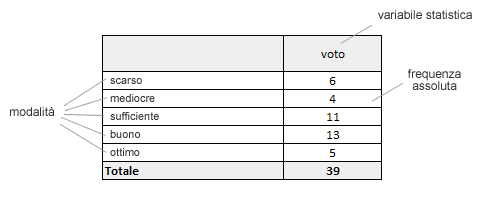
Le celle della matrice dove si incontrano le righe e le colonne sono utilizzate per rappresentare la frequenza con cui si è presentata quella modalità della variabile statistica. Per semplificare la rappresentazione, le modalità di tipo quantitativo possono anche essere raggruppate in classi.
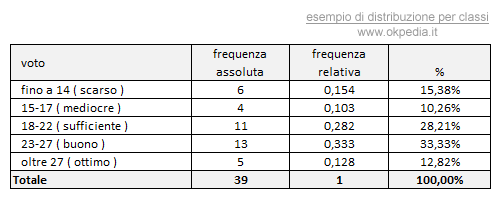
Ad esempio, si potrebbe dedicare una riga per ogni voto da zero a trenta, ma è molto più comodo raggrupparli e indicarli in una sola riga e in un'unica classe ( "fino a 14" ). E così via.
La rappresentazione grafica dei dati statistici
Nella rappresentazione grafica le distribuzioni di frequenza sono elaborate in modo visivo, sotto forma di poligoni ed elementi geometrici. Questa tipologia di rappresentazione è più efficace poiché permette di comprendere in modo visivo, a colpo d'occhio, l'informazione contenuta nei dati. Esistono diverse tipologie di grafici.
Gli istogrammi
Un istogramma è un grafico che si sviluppa verso l'alto. Il termine nasce dall'unione delle parole greche histós ( trama ) e graphein ( disegnare ). È anche conosciuto come diagramma a barre.
In un istogramma la distribuzione delle frequenze è rappresentata mediante dei rettangoli all'interno degli assi cartesiani. Nell'asse delle ascisse sono elencate le modalità mentre nell'asse delle ordinate sono misurate le frequenze per ciascuna modalità.
Un istogramma può essere utilizzato anche per la rappresentazione della distribuzione per classi di frequenze. In questo caso, la base orizzontale del rettangolo indica la classe di frequenza mentre l'altezza è pari alla somma delle frequenze ( assolute o relative ).
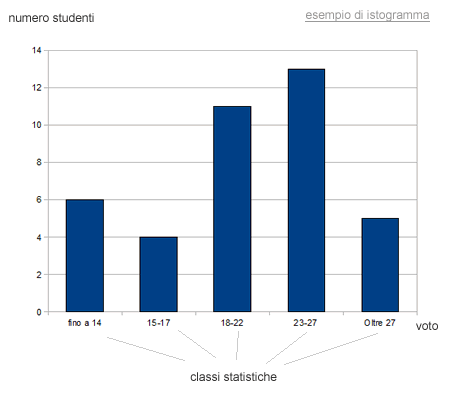
L'altezza dei rettangoli è proporzionale alla frequenza assoluta secondo una comune scala di misurazione che viene applicata su tutto il grafico. Il rapporto tra l'altezza dei rettangoli e la frequenza è detto coefficiente di proporzionalità del grafico.
Ad esempio, in un grafico con coefficiente di proporzionalità pari a uno, l'altezza del rettangolo è uguale alla frequenza assoluta della classe. La scala varia a seconda del tipo di analisi e non è sempre possibile applicare un coefficiente di proporzionalità pari a uno.
Gli istogrammi con classi di diversa ampiezza
Quando le classi hanno diversa ampiezza è possibile rappresentare un istogramma associando a ciascun rettangolo una base di lunghezza diversa, pari all'ampiezza della classe.
In questo caso, l'altezza di ogni rettangolo è calcolata dividendo la frequenza assoluta per il l'ampiezza della classe. La superficie di ogni rettangolo deve essere proporzionale alla frequenza assoluta della classe.
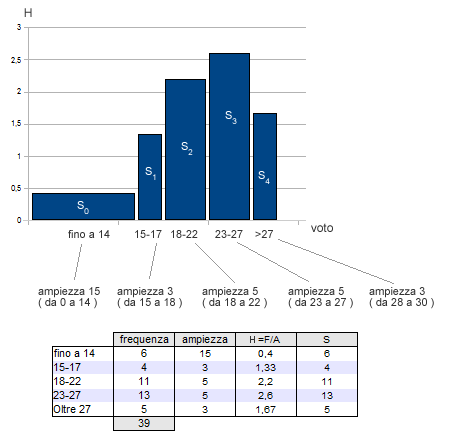
Ad esempio, la prima classe ha un'ampiezza (A) pari a 15 e un'altezza (H) pari a 0,4. La superficie del rettangolo (AxH) è quindi pari a 6 ed è uguale alla frequenza della classe.
Gli stereogrammi o diagrammi in tre dimensioni
Gli stereogrammi sono diagrammi a barre tridimensionali. Questa rappresentazione è simile agli istogrammi tradizionali ma si presenta con una qualità estetica superiore. In sostituzione delle figure rettangolari su due dimensioni, in uno stereogramma la frequenza viene rappresentata tramite figure geometriche solide.
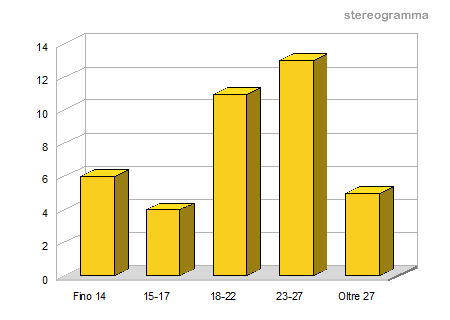
Il grafico a linea
Il grafico a linea è un altra forma di rappresentazione dei dati. Il grafico è composto da una linea spezzata che congiunge le frequenze delle classi in un diagramma cartesiano. Sul piano cartesiano le classi sono indicate sull'asse delle ascisse, mentre le frequenze sono misurate sull'asse delle ordinate.
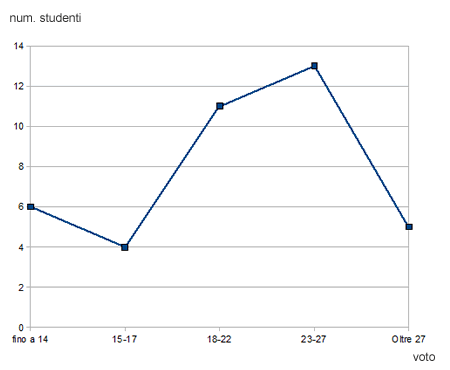
Il grafico a linee appartiene alla categoria dei poligoni di frequenza.
Le ogive cumulate e retrocumulate
Un grafico a linea spezzata può essere utilizzato anche per misurare la distribuzione delle frequenze cumulate o retrocumulate di una serie statistica. In questo caso, la linea spezzata cumulata è detta ogiva.
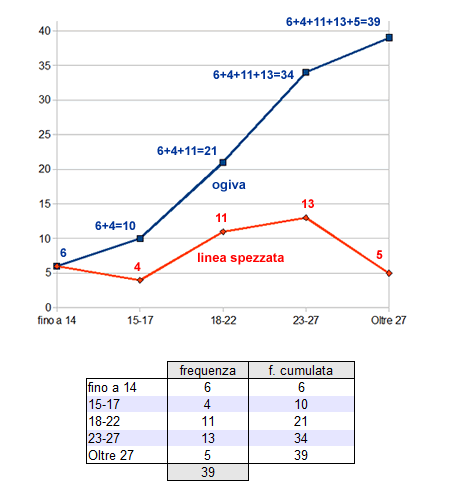
Nel caso delle frequenze cumulate l'ogiva misura le frequenze dalla prima classe all'ultima, assumendo un andamento crescente, dal basso verso l'alto. Viceversa, nel caso delle frequenze retrocumulate l'ogiva computa il cumulo a partire dall'ultima classe e assume un andamento decrescente, dall'alto verso il basso.
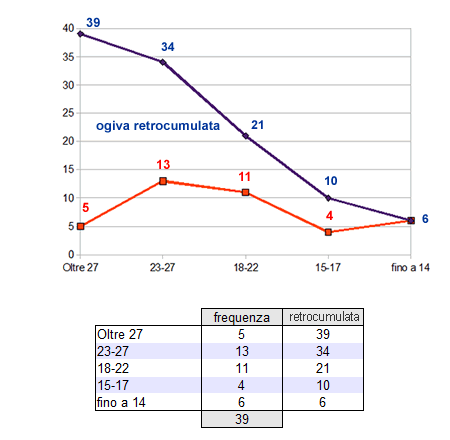
I cartogrammi
I cartogrammi sono rappresentazioni grafiche che consentono di osservare la distribuzione delle frequenze in un territorio geografico. Sono costruiti applicando su una mappa dei simboli o delle colorazioni diverse. Ogni simbolo o colore indica una particolare classe di frequenza.
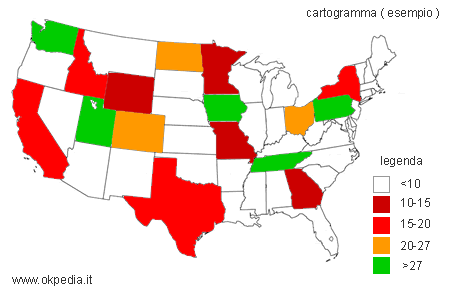
L'interpretazione delle informazioni in un cartogramma è resa possibile dalla presenza di una legenda, ove le colorazioni sono associate alle diverse classi di frequenza del fenomeno osservato.
Il diagramma a torta
I diagramma a torta sono utilizzati per rappresentare le distribuzioni di frequenza in un cerchio che rappresenta il totale del fenomeno. Il cerchio viene suddiviso in tante parti, quante sono le classi di frequenza o le modalità del fenomeno, e ogni parte ha un colore differente dalle altre.
L'angolo giro del cerchio (360%) eguaglia il 100% della totalità del fenomeno. L'angolo al centro di ogni singola parte è, quindi, proporzionale all'intensità del fenomeno nella rispettiva classe di frequenza.
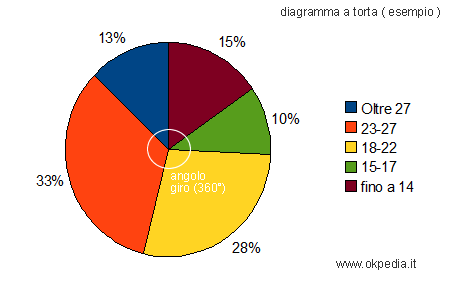
Ad esempio, il 13% degli studenti con un voto al di sopra di 27 è rappresentato dal settore blu. Il 33% degli studenti con un voto compreso tra 23 e 27 sono rappresentati dal settore arancione con un'angolazione proporzionalmente superiore rispetto alla precedente.
Il diagramma è detto "a torta" in quanto ogni singola suddivisione ha la forma di un pezzo di torta. È uno strumento particolarmente efficace per rappresentare le frequenze relative percentuali di una variabile statistica.
Gli ideogrammi
Un ideogramma utilizza un'immagine per rappresentare e misurare un fenomeno. L'immagine viene scelta per agevolare l'interpretazione dell'informazione da parte del lettore. Ad esempio, per misurare la popolazione si può utilizzare l'immagine stilizzata di una persona.
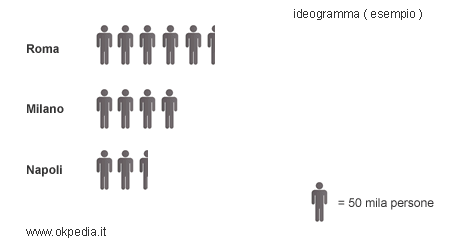
Gli ideogrammi consentono di misurare un fenomeno mediante la ripetizione dell'immagine, in modo proporzionale alla sua frequenza, secondo una particolare scala di riferimento. Ad esempio, ogni immagine di una persona equivale a 500 mila abitanti.
L'uso degli ideogrammi rende l'interpretazione dei dati particolarmente semplice, poiché il lettore associa più rapidamente la misura quantitativa all'informazione.
