Mediana
In statistica la mediana è un indice sintetico di posizione che restituisce il valore mediano di una distribuzione.
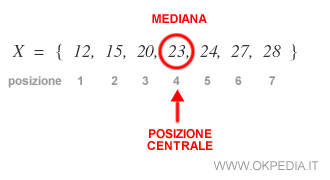
Il valore mediano è l'unità che occupa la posizione centrale nella distribuzione ordinata dei valori.
La mediana può essere calcolata in una distribuzione quantitativa ( es. 1,2,3,4, ... ) o qualitativa ordinabile.
La formula della mediana
La posizione della mediana di un insieme di N numeri ordinati in modo progressivo è la seguente.
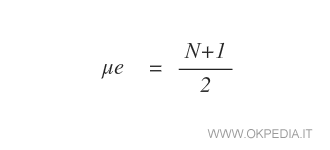
La variabile N indica il numero dei valori contenuti nella distribuzione.
Un esempio pratico
La seguente distribuzione è composta da sette unità ( N=7 ).

Pertanto, il valore mediano si trova alla quarta posizione ed è pari a 23.
Come calcolare la mediana
Per calcolare la mediana di una distribuzione di valori si procede nel seguente modo.
Data una distribuzione quantitativa X
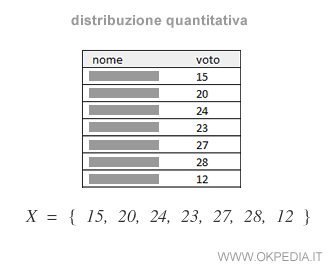
bisogna ordinare i valori in ordine crescente ( o decrescente ).
Si forma così una seriazione.

La mediana è il valore che occupa la posizione a metà della distribuzione statistica.
In questo caso il valore mediano è 23.

La mediana è indicata con il simbolo μe.
Pertanto scriveremo:
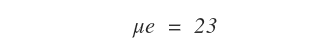
Nota. Se la distribuzione è composta da un numero dispari di valori, la mediana è una e una sola. Viceversa, se è composta da un numero pari di valori esistono due valori mediani ( inferiore e superiore ).

In questi casi per avere un unico valore mediano si può calcolare la media aritmetica della mediana inferiore e superiore. Nell'esempio precedente il valore mediano è 22 ( la media aritmetica di 20 e 24 ).
I vantaggi della mediana rispetto alla media
A differenza della media aritmetica, la mediana non è influenzata dalla presenza di dati anomali.
Esempio. La presenza di un valore molto più grande o più piccolo degli altri nella distribuzione X non modifica la mediana. Viceversa, influisce sulla media aritmetica.
Nella precedente distribuzione X sostituiamo l'ultimo valore con 200.
E' molto più grande degli altri. Pertanto è un valore anomalo.
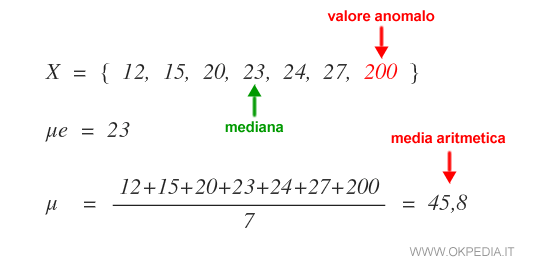
Il valore anomalo non modifica il valore mediano ma modifica sensibilmente la media aritmetica.
In questi casi la mediana ( 23 ) è più rappresentativa della distribuzione X rispetto alla media aritmetica ( 45,8 ).
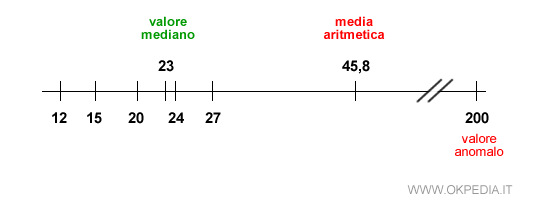
La mediana rappresenta meglio la distribuzione dei valori { 12, 15, 20, 23, 24, 27, 200 }.
La mediana di una distribuzione qualitativa
La mediana può essere calcolata anche in una distribuzione qualitativa, purché le modalità siano ordinabili secondo un criterio oggettivo.
Un esempio di distribuzione qualitativa ordinabile sono i voti scolastici: "scarso, mediocre, sufficiente, distinto, ottimo".

Le modalità sono qualitative ma ordinabili secondo un criterio progressivo logico.
Esempio. Nella modalità voto il dato "scarso" vale meno di "mediocre". Il dato "mediocre" vale meno di "sufficiente". E così via. C'è un ordine di preferenza anche se i valori non sono quantitativi.
Pertanto, è possibile calcolare la mediana.
Nella tabella precedente il valore mediano è "sufficiente"
Viceversa, se le modalità della distribuzione qualitativa non sono ordinabili, non può essere calcolata la mediana.
