Istanziazione esistenziale
L'istanziazione esistenziale è una regola di sostituzione di una variabile x in una formula f(x) con il simbolo di una nuova costante C detta costante di Skolem. L'istanziazione esistenziale consente di trasformare una formula logica della logica del primo ordine, in cui sia presente il quantificatore esistenziale (∃), in una formula logica della logica proposizionale.
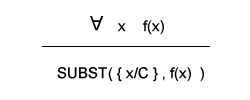
Ad esempio, in una base di conoscenza è presente la formula logica quantificata esistenzialmente che afferma "esiste almeno un vescovo che è anche pontefice". La formula è caratterizzata dal quantificatore esistenziale "esiste almeno un".
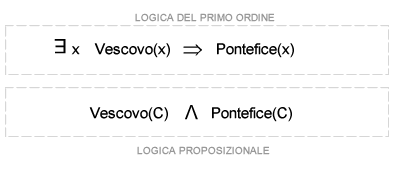
La regola di istanziazione esistenziale sostituisce la formula logica del primo ordine in una istanza della logica proposizionale, sostituendo la variabile x con il simbolo della nuova costante C. L'istanziazione esistenziale è una delle principali tecniche di proposizionalizzazione.
- Nome della costante. Per evitare problemi di analisi è necessario assegnare alla costante di Skolem un simbolo non utilizzato anche dalle altre variabili. E' utile riservare una famiglia di simboli ( es. C ) esclusivamente alle costanti di Skolem. In questo modo le variabili del problema possono essere definite con tutti i simboli, fatta eccezione che per quelli riservati alle costanti di Skolem.
