Inferenza per sostituzione ( unificazione )
L'inferenza per sostituzione è una tecnica di inferenza della logica del primo ordine. Data una formula logica ( regola ) in cui sia presente una premessa ( insieme di condizioni ) e una conclusione, per rispondere a una query l'algoritmo seleziona i dati ( termini ground ) che rendono veri tutti i congiunti della premessa e li sostituisce alla variabile della formula. Il processo che rende vere le diverse espressioni logiche è detto processo di unificazione. Ad esempio, data una popolazione di tre persone ( Tizio, Caio, Sempronio ) e da cinque regole ( formule logiche ), l'utente chiede alla base di conoscenza quali persone conosce Tizio. Nella logica del primo ordine la formula della query è rappresentata nella forma Conosce ( Tizio, y ) dove "Conosce" è una funzione logica ( predicato ) con due argomenti e la lettera y è la variabile incognita.
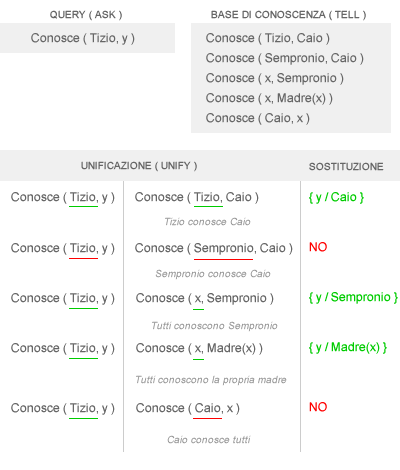
Il processo di unificazione ( UNIFY ) compara la formula della query con quelle presenti nella base di conoscenza. Per comprendere il funzionamento dell'algoritmo di inferenza logica del primo ordine è consigliabile seguire il ragionamento per ogni singolo passo:
- Tizio conosce Caio. Nella prima formula Conosce ( Tizio, Caio ) si verifica una sostituzione piena, in quanto nella base di conoscenza è già noto che Tizio conosce Caio. È una dichiarazione esplicita precedentemente inserita nella base di conoscenza tramite un comando Tell.
- Sempronio conosce Caio. Nella seconda formula Conosce ( Sempronio, Caio) l'unificazione fallisce poiché non esiste alcun valore nel primo argomento ( Tizio ≠ Sempronio ).
- Tutti conoscono Sempronio. Nella terza formula Conosce ( x, Sempronio ) troviamo l'affermazione "Tutti conoscono Sempronio". È quindi possibile sostituire la variabile x con Tizio per soddisfare l'unificazione. Possiamo, quindi, affermare che Tizio conosce Sempronio anche senza avere un'esplicita affermazione a riguardo nella base di conoscenza.
- Tutti conoscono la propria madre. Nella quarta formula Conosce ( x, Madre(x) ) l'algoritmo apprende che tutti conoscono la propria madre. È quindi sufficiente sostituire la variabile x con Tizio per sapere che Tizio conosce anche la propria madre ( Madre(Tizio ) ).
- Caio conosce tutti. Nella quinta formula Conosce ( Caio, x ) si apprende dalla base di conoscenza che Caio conosce tutti. Non essendoci alcuna coincidenza possibile nel primo argomento delle due formule ( Tizio ≠ Caio ), il processo di unificazione fallisce.
In conclusione, al termine del processo di unificazione l'algoritmo può rispondere alla domanda "chi conosce Tizio" con la seguente risposta: "Tizio conosce Caio, Tizio conosce Sempronio e Tizio conosce sua madre".
- Esempio. Il processo di unificazione può essere utilizzato per rispondere a qualsiasi altra domanda. Ad esempio, chiedendo alla base di conoscenza quali persone conosce Sempronio, l'algoritmo risponde che Sempronio conosce Caio, conosce se stesso (inutile) e conosce la propria madre. È però possibile formulare anche altre domande, ad esempio "chi conosce Tizio?", "quali persone conoscono Tizio?", "quante persone non conoscono Sempronio?", ecc. Nella seguente rappresentazione viene mostrato il processo di unificazione per la domanda "quali persone conosce Sempronio?"

- Indicizzazione dei predicati. Il processo inferenziale può essere notevolmente migliorato tramite l'indizzazione dei predicati. In questo modo l'algoritmo non deve più ricercare le unificazioni su tutta la lista delle formule atomiche ma soltanto su quella del predicato desiderato.
