Sistema caotico
Un sistema caotico è un sistema dinamico fortemente dipendente dalle condizioni iniziali e con una evoluzione non lineare. Tali caratteristiche lo rendono imprevedibile.
Una variazione infinitesimale nelle condizioni iniziali determina variazioni importanti sia sui risultati in uscita e sia sull'evoluzione del sistema caotico nel corso del tempo.
Le caratteristiche dei sistemi caotici
A causa della forte dipendenza dalle condizioni iniziali (o condizioni di ambiente) l'evoluzione di un sistema caotico non è prevedibile con largo anticipo.
Un sistema caotico è un sistema complesso e imprevedibile
Esempio. Un esempio di sistema caotico sono i fenomeni meteorologici. Pur conoscendo tutte le variabili del sistema meteo, è sufficiente un piccolo errore di misura nelle condizioni iniziali per condurre a previsioni errate. Per questa ragione è quasi impossibile effettuare previsioni meteo a lungo termine.
Il sistema caotico è studiato in fisica e in matematica ed è alla base della teoria del caos.
Esempio di sistema caotico
Per fare un esempio pratico prendiamo la seguente funzione caotica:
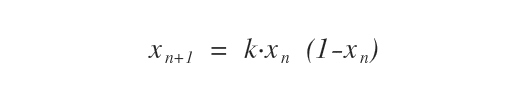
Poi usiamo due diverse condizioni iniziali alla variabile X0.
- X0 = 0,5. Nel primo caso partiamo dal valore iniziale X0 = 0,5
- X0 = 0,77. Nel secondo partiamo dal valore iniziale X0 = 0,77.
Cambiando il valore iniziale ( X0 ) il grafico della funzione ha un'evoluzione completamente differente nel tempo.
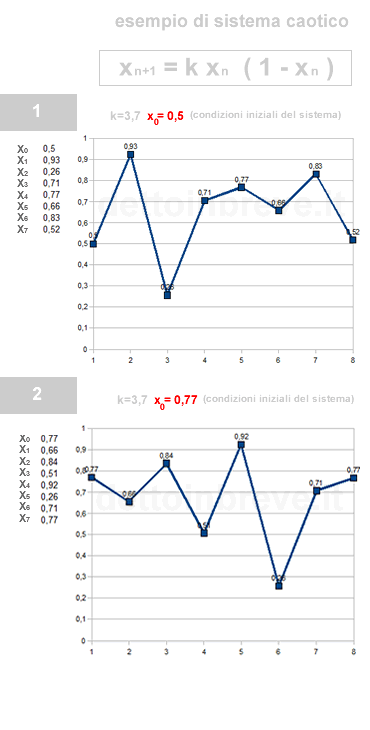
La rappresentazione grafica della funzione dimostra l'imprevedibilità del sistema caotico.
Una piccola variazione alle condizioni iniziali modifica sensibilmente l'evoluzione futura del sistema.
In entrambi i casi l'evoluzione del sistema è caotica ( non lineare ).
Le applicazioni dei sistemi caotici
L'imprevedibilità e l'apparente disordine nell'evoluzione dei risultati potrebbe erroneamente far pensare all'inutilità dei sistemi caotici. In realtà non è così.
Un sistema caotico potrebbe intepretare meglio la complessità della realtà rispetto a un semplice sistema matematico lineare.
L'uso dei sistemi caotici è particolarmente efficace nell'analisi dei sistemi complessi ( meteo, finanza, crescita della popolazione ecc. ) e ottiene buoni risultati nello sviluppo dei modelli previsionali.
