L'orizzonte degli eventi
L'orizzonte degli eventi è una zona di forma sferica situata intorno a un buco nero, oltrepassata la quale un corpo non può più sfuggire alla forza gravitazionale del black hole.
Nell'orizzonte degli eventi la velocità di fuga è pari alla velocità della luce. Ne consegue che nemmeno la luce può sfuggire all'attrazione gravitazionale del buco nero.
Perché si dice orizzonte degli eventi?
Un osservatore esterno può osservare soltanto gli "eventi" che si verificano prima dell'orizzonte. Tutti gli eventi che accadono oltre l'orizzonte non sono osservabili, poiché la velocità di fuga dal buco nero è enorme, e non possono più influenzare l'osservatore esterno. Per questo motivo si dice "orizzonte".
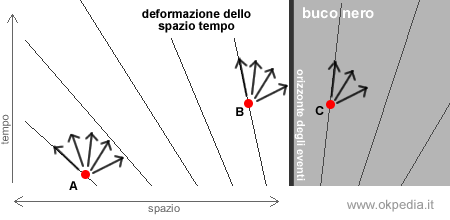
La forza di gravità del buco nero deforma lo spazio-tempo. Quanto più una particella si avvicina all'orizzonte temporale, tante meno esistono delle vie di allontanamento. All'interno del buco nero, tutti i percorsi dello spazio conducono verso il centro del black hole.
Qual è la forma dell'orizzonte?
In un buco nero non rotante e privo di carica elettrica, l'orizzonte assume una forma sferica. Questo caso è anche conosciuto come buco nero di Schwarzschild.
Qual è la distanza dell'orizzonte dal buco nero?
L'orizzonte degli eventi è direttamente proporzionale alla massa (M) del buco nero e inversamente proporzionale alla velocità della luce (c). Il raggio dell'orizzonte in un buco nero non rotante è la seguente:
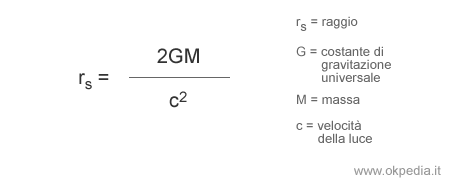
Questo raggio è anche detto raggio di Schwarzschild.
