Logaritmo
Il logaritmo di un numero N in una base B è l'esponente X a cui si deve elevare B per ottenere N.
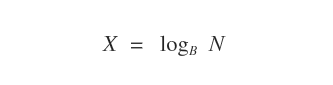
Il numero N è detto argomento del logaritmo.
Le condizioni del logaritmo sono le seguenti. La base B e il numero N devono essere numeri reali positivi ( maggiori di zero ). Inoltre, la base B deve essere diversa da uno.
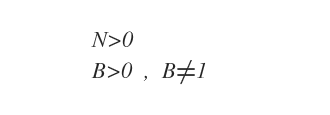
Cosa sono i logaritmi
I logaritmi sono una forma alternativa per rappresentare le potenze.
Il logaritmo rappresenta in modo differente la relazione tra la base, l'esponente e il risultato della potenza.
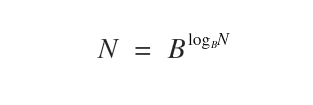
A cosa servono i logaritmi? I logaritmi sono introdotti dal matematico scozzese Nepero nel XVII secolo per semplificare il calcolo con i numeri molto grandi, tramite l'utilizzo delle tavole dei logaritmi.
Un esempio pratico di logaritmo
Una qualsiasi potenza è composta da una base e da un esponente.
La potenza è l'operazione che associa la base e l'esponente al numero pari al prodotto di n fattori uguali alla base.
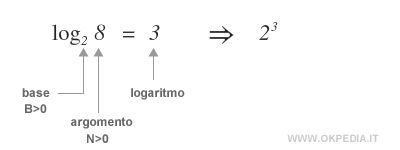
Ad esempio, il numero 2 elevato all'esponente 4 è uguale a 16.
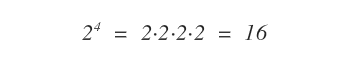
Pertanto, la stessa relazione di potenza può essere descritta tramite un logaritmo nella seguente forma:
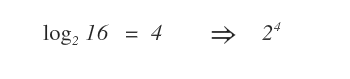
Il logaritmo è l'esponente (4) della potenza su base 2 che consente di ottenere come risultato il numero 16.
In altri termini, il logaritmo è il numero di volte che la base deve essere moltiplicata per se stessa per ottenere come risultato il numero 16.
La differenza tra logaritmi decimali e naturali
Esiste un insieme infinito di sistemi di logaritmi che hanno per base un numero reale positivo qualsiasi.
Un sistema di logaritmi è l'insieme dei logaritmi di tutti i numeri reali positivi con la stessa base.
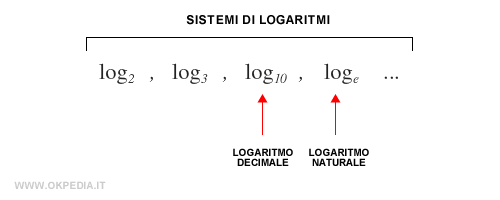
Tra questi, due sistemi di logaritmi sono particolarmente importanti:
- Il logaritmo decimale è il logaritmo calcolato su base 10. Sono indicati con log X senza indicare la base.
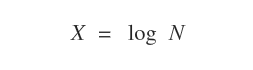
- Il logaritmo naturale è il logaritmo calcolato su base e=2.71828182845... Sono anche detti logaritmi neperiani o logaritmi iperbolici e sono indicati con ln x.
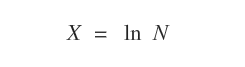
Se non è indicata la base del logaritmo, per convenzione si tratta un logaritmo decimale. La base 10 del logaritmo si sottintende. Pertanto, scrivere log 5 equivale a scrivere log10 5.
La funzione logaritmica
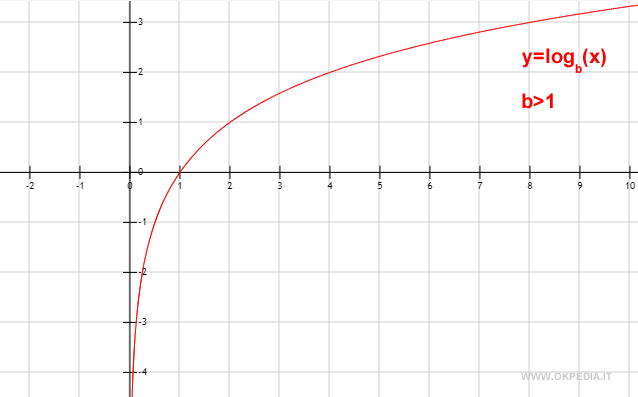
Se la base del logaritmo è maggiore di uno (B>1), la funzione logaritmica è una funzione crescente in R+.
Al crescere dell'argomento, aumenta il logaritmo.
Un esempio pratico
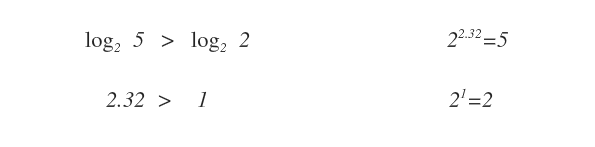
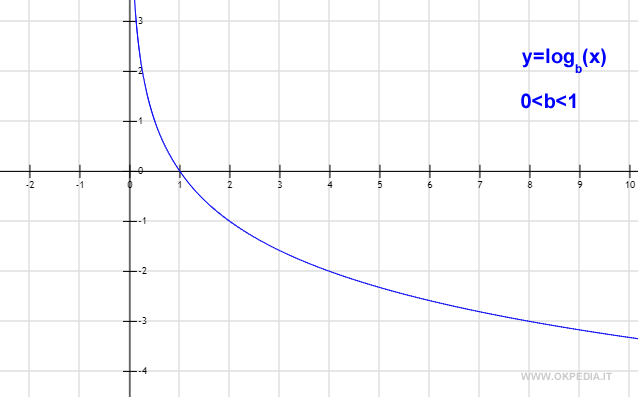
Se la base del logaritmo è compresa tra zero e uno (0<B<1), la funzione logaritmica è una funzione decrescente in R+.
Al crescere dell'argomento, si riduce il logaritmo.
Un esempio pratico
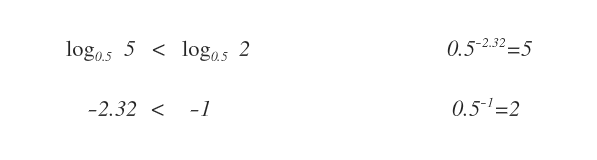
- Esiste un logaritmo in base zero?
No, perché zero (B=0) elevato a qualsiasi numero positivo (X>0) dà come risultato sempre zero (N=0). - Esiste un logaritmo in base uno?
No, perché uno (B=1) elevato a qualsiasi numero positivo (X>0) dà come risultato sempre uno (N=1). - Il logaritmo può essere negativo?
Si, un logaritmo può essere sia positivo che negativo. Ad esempio, se la base è minore di 1 (B<1) e l'argomento è maggiore di 1 (N>1), il logaritmo è sempre negativo (X<0).
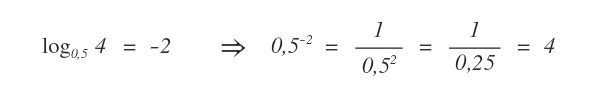
Nota. Il logaritmo può essere anche negativo ma l'argomento del logaritmo è sempre positivo. L'argomento del logaritmo non può essere nullo o negativo.
- Quando il logaritmo è sicuramente positivo?
Se sono maggiori di uno la base (B>1) e l'argomento (N>1) allora l'esponente ( logaritmo ) è sicuramente positivo (X>0).
- Qual è il segno del logaritmo?
Occorre distinguere due casi:
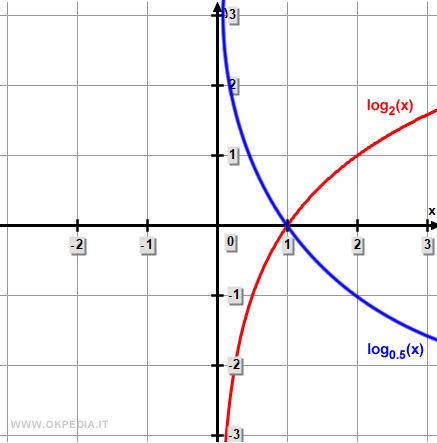
A] Se la base è maggiore di uno (B>1) il logaritmo è negativo nell'intervallo (0,1) e positivo nell'intervallo da (1, +∞). Il logaritmo è in funzione crescente rispetto all'argomento. Nel grafico è la linea rossa.
B] Se la base è inferiore di uno e maggiore di zero (0<B<1) il logaritmo è positivo nell'intervallo (0,1) e negativo nell'intervallo da (1, +∞). Il logaritmo è decrescente rispetto all'argomento. Nel grafico è la linea blu.
