Algoritmo back propagation ( reti neurali )
L'algoritmo di back propagation è un algoritmo di apprendimento delle reti neurali. L'algoritmo confronta il valore in uscita del sistema con il valore desiderato ( obiettivo ). Sulla base della differenza così calcolata ( errore ), l'algoritmo modifica i pesi sinaptici della rete neurale, facendo convergere progressivamente il set dei valori di uscita verso quelli desiderati. Ad esempio, data una rete neurale con un solo nodo N e una sola entrata X, il sistema ha l'obiettivo di raggiungere un determinato livello di uscita YD. Al termine di ogni ciclo, l'algoritmo confronta il risultato ottenuto Y con quello desiderato YD e calcola un errore YD-Y (e). Una retroazione ( feedback ) consente all'algoritmo di utilizzare l'errore per aggiustare il peso sinaptico pt ed eseguire una nuova iterazione ( back-propagation o propagazione all'indietro ).
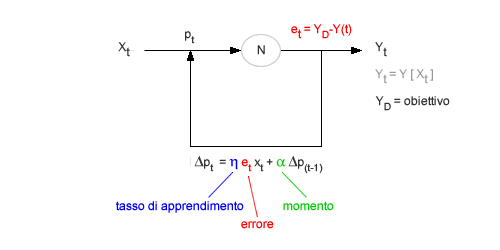
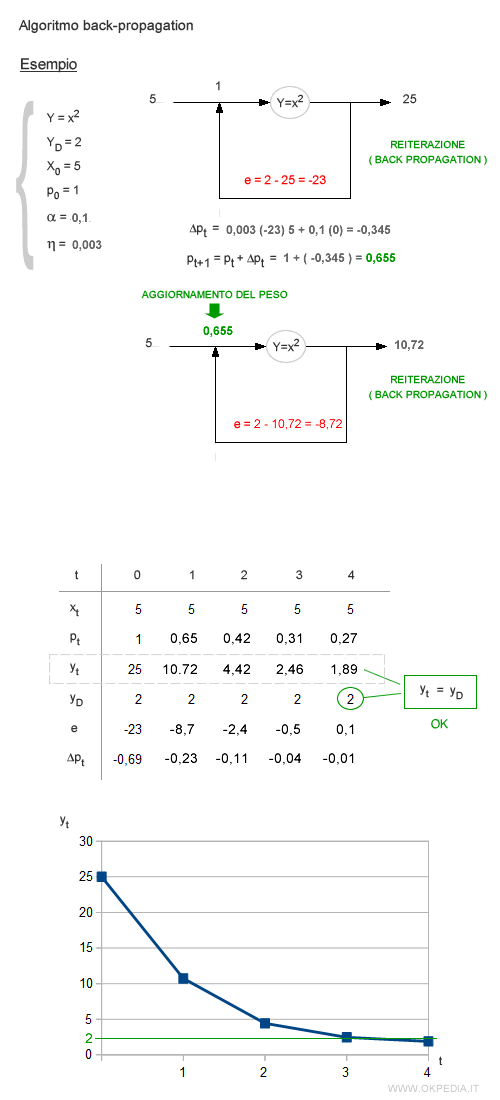
L'aggiustamento del peso sinaptico è determinato dall'errore e da due parametri del sistema: il tasso di apprendimento e il momento. Entrambi i parametri possono variare da zero a uno ( 0 - 1 ). Il tasso di apprendimento influenza la velocità del processo apprendimento. Quanto più è elevato il tasso di apprendimento, vicino al valore massimo uno, tanto più veloce è il processo di apprendimento, in quanto sono più grandi le variazioni da apportare sul peso sinaptico. Tuttavia, un tasso di apprendimento molto alto aumenta anche il rischio delle variazione erratiche ( oscillazioni del risultato ) e, quindi, l'instabilità del sistema. Per ridurre le oscillazioni e favorire la convergenza dei risultati, nella formula di aggiustamento del peso sinaptico si utilizza un secondo parametro ( α ), detto momento, anch'esso compreso tra zero e uno (0-1). Nel seguente esempio è mostrato un processo dinamico di apprendimento dell'algoritmo a partire da una situazione iniziale ( x=5 ). Nella situazione iniziale il peso sinaptico è fissato casualmente ed è pari al valore uno ( p=1 ). In cinque reiterazioni l'algoritmo modifica progressivamente il peso sinaptico pt fino a raggiungere l'obiettivo desiderato ( Yd=2 ). Dopo la quinta iterazione la rete neurale è nuovamente stabile e il peso sinaptico permane costante al valore di equilibrio ( pt=0,08 ). Per semplicità espositiva ipotizziamo che il segnale in entrata resti costante ( x=5 ) durante l'intero processo di aggiustamento del peso sinaptico ( processo di apprendimento ).
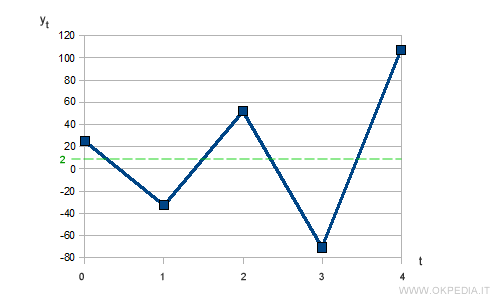
Non è però detto che l'algoritmo raggiunga sempre le condizioni di equilibrio. Ad esempio, se il tasso di apprendimento è troppo alto in alcuni problemi il processo di aggiustamento diventa divergente e oscillante intorno all'obiettivo. Pertanto, l'algoritmo non raggiunge mai l'equilibrio, perché le oscillazioni sono sempre più grandi.
 Complessità dell'algoritmo. La complessità dell'algoritmo di back propagation cresce con la dimensione della rete neurale. Quando la rete neurale è composta da pochi neuroni si verifica il problema dell'underfitting e il processo di apprendimento della rete potrebbe essere inefficace. Viceversa, quando la rete è composta da molti neuroni si verifica il problema dell'overfitting facendo diventare più difficoltoso il processo di generalizzazione.
Complessità dell'algoritmo. La complessità dell'algoritmo di back propagation cresce con la dimensione della rete neurale. Quando la rete neurale è composta da pochi neuroni si verifica il problema dell'underfitting e il processo di apprendimento della rete potrebbe essere inefficace. Viceversa, quando la rete è composta da molti neuroni si verifica il problema dell'overfitting facendo diventare più difficoltoso il processo di generalizzazione.
- Pattern. Il pattern è l'insieme dei valori di input possibili del sistema.
- Epoca. L'epoca è una singola iterazione dell'algoritmo di apprendimento. In ogni epoca ( iterazione ) l'algoritmo verifica il valore di uscita ( set di valori di uscita ) con il valore desiderato ( set di valori desiderati ) al fine di calcolare l'errore del sistema.
- Back-propagation. La propagazione all'indietro ( propagazione a ritroso ) è il collegamento di feedback che utilizza l'errore del sistema per aggiustare il valore dei pesi sinaptici della rete neurale. La retroazione dovrebbe consentire al sistema di ridurre progressivamente l'errore ( minimizzazione del gradiente ), in modo tale da far convergere il valore in uscita del sistema verso il livello desiderato.
- Minimo locale. L'algoritmo è esposto al rischio dei minimi locali. In caso di presenza di un minimo locale, l'algoritmo potrebbe non essere in grado di uscirne, restituendo come risultato finale un valore sub-ottimale ( minimo locale ) anziché un valore ottimale ( minimo globale ).
