Funzioni reali
Una funzione reale è una funzione y=f(x) in cui il dominio e il codominio sono sottoinsiemi dell'insieme dei numeri reali R.
La funzione di una variabile reale f(x) associa a ogni valore x del dominio uno e un solo valore y del codominio.
L'insieme delle coppie (x,y) di una funzione reale può essere rappresentata su un diagramma cartesiano tramite il grafico della funzione.
Ogni coppia (x,y) individua un punto del piano cartesiano.
Nota. I primi studi sulle funzioni reali sono attribuiti a Eulero e Lagrange nel XVIII secolo.
Esempio
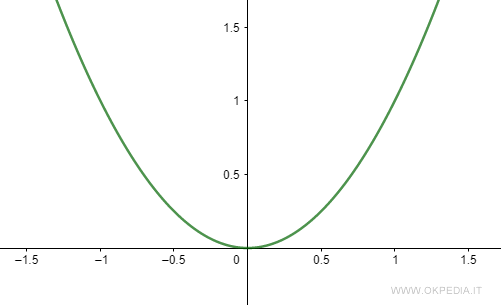
La funzione f(x)=x2 è una funzione reale.
y = f(x) = x2
Il dominio è l'insieme dei numeri reali mentre il codominio è un sottoinsieme dei numeri reali.
Il grafico della funzione è il seguente